
【题目】已知椭圆曲线方程为 ![]() ,两焦点分别为F1 , F2 .
,两焦点分别为F1 , F2 .
(1)若n=﹣1,过左焦点为F1且斜率为 ![]() 的直线交圆锥曲线于点A,B,求△ABF2的周长.
的直线交圆锥曲线于点A,B,求△ABF2的周长.
(2)若n=4,P圆锥曲线上一点,求PF1PF2的最大值和最小值.
【答案】
(1)
解:若n=1,方程为x2﹣y2=1,则直线AB的方程为y= ![]() (x+
(x+ ![]() ).
).
联立x2﹣y2=1,可得2x2+6 ![]() x+7=0,∴|AB|=
x+7=0,∴|AB|= ![]() =4,
=4,
据双曲线定义,2a=|AF2|﹣|AF1|=|BF2|﹣|BF1|,
∴4a=|AF2|+|BF2|﹣(|AF1|+|BF1|)=4,
∴|AB|+|AF2|+|BF2|=12
(2)
解:若n=4,方程为 ![]() =1,
=1,
∴PF1+PF2=4,
设PF1=x,x∈[2﹣ ![]() ,2+
,2+ ![]() ],
],
∴PF1PF2=x(4﹣x)=﹣(x﹣2)2+4,
∴PF1PF2的最大值为4,最小值为1
【解析】(1)求出|AB|,利用双曲线的定义,即可求△ABF2的周长.(2)若n=4,P圆锥曲线上一点,PF1+PF2=4,设PF1=x,x∈[2﹣ ![]() ,2+
,2+ ![]() ],PF1PF2=x(4﹣x)=﹣(x﹣2)2+4求,即可PF1PF2的最大值和最小值.
],PF1PF2=x(4﹣x)=﹣(x﹣2)2+4求,即可PF1PF2的最大值和最小值.
【考点精析】本题主要考查了椭圆的概念的相关知识点,需要掌握平面内与两个定点![]() ,
,![]() 的距离之和等于常数(大于
的距离之和等于常数(大于![]() )的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距才能正确解答此题.
)的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知命题p:函数 ![]() 在区间(m,m+1)上单调递减,命题q:实数m满足方程
在区间(m,m+1)上单调递减,命题q:实数m满足方程 ![]() 表示的焦点在y轴上的椭圆.
表示的焦点在y轴上的椭圆.
(1)当p为真命题时,求m的取值范围;
(2)若命题“p且q”为假命题,“p或q”为真命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(1﹣a)x+(1﹣a).a∈R.
(1)当a=4时,解不等式f(x)≥7;
(2)若对P任意的x∈(﹣1,+∞),函数f(x)的图象恒在x轴上方,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆 ![]() (m>n>0)的离心率e的值为
(m>n>0)的离心率e的值为 ![]() ,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P.
,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P. 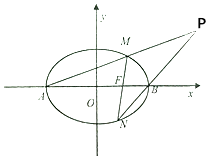
(1)求椭圆的标准方程;
(2)若点P(4, ![]() ),直线AN,BM的斜率分别为k1 , k2 , 求
),直线AN,BM的斜率分别为k1 , k2 , 求 ![]() .
.
(3)求证点P在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() ,若f(x)≤g(x)在区间[0,1]上恒成立,则( )
,若f(x)≤g(x)在区间[0,1]上恒成立,则( )
A.实数t有最小值1
B.实数t有最大值1
C.实数t有最小值 ![]()
D.实数t有最大值 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】建造一间地面面积为12m2的背面靠墙的猪圈,底面为长方形的猪圈正面的造价为120元/m2 , 侧面的造价为80元/m2 , 屋顶造价为1120元.如果墙高3m,且不计猪圈背面的费用,问怎样设计能使猪圈的总造价最低,最低总造价是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 则异面直线BA1与AC1所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com