
【题目】已知函数![]() ,任取
,任取![]() ,记函数
,记函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() 最小值为
最小值为![]() 记
记![]() . 则关于函数
. 则关于函数![]() 有如下结论:
有如下结论:
①函数![]() 为偶函数;
为偶函数;
②函数![]() 的值域为
的值域为![]() ;
;
③函数![]() 的周期为2;
的周期为2;
④函数![]() 的单调增区间为
的单调增区间为![]() .
.
其中正确的结论有____________.(填上所有正确的结论序号)
【答案】③④.
【解析】
试题因为![]() ,其中
,其中![]() 分别是指函数
分别是指函数![]() 在区间
在区间![]() 上的最大值、最小值,注意到函数
上的最大值、最小值,注意到函数![]() 是最小正周期为
是最小正周期为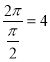 的函数,所以
的函数,所以![]() 在区间
在区间![]() 的图像与在
的图像与在![]() 的图像完全相同,所以
的图像完全相同,所以![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 的一个周期为4,对该函数性质的研究,只须先探究
的一个周期为4,对该函数性质的研究,只须先探究![]() 的性质即可.
的性质即可.
根据![]() 的图像(如下图(1))与性质可知
的图像(如下图(1))与性质可知
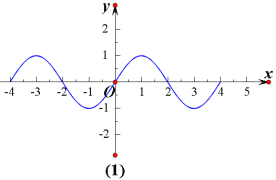
当![]() 时,
时,![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,此时
,此时![]()
当![]() 时,
时,![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,最大值为1,此时
,最大值为1,此时![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,最大值为1,此时
,最大值为1,此时![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,此时
,此时![]()
作出![]() 的图像,如下图(2)所示
的图像,如下图(2)所示

综上可知,该函数没有奇偶性,函数的值域为![]() ,从图中可以看到函数的最小正周期为2,函数的单调递增区间为
,从图中可以看到函数的最小正周期为2,函数的单调递增区间为![]() ,故只有③④正确.
,故只有③④正确.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】某企业生产某种商品![]() 吨,此时所需生产费用为
吨,此时所需生产费用为![]() 万元,当出售这种商品时,每吨价格为
万元,当出售这种商品时,每吨价格为![]() 万元,这里
万元,这里![]() (
(![]()
![]() 为常数,
为常数,![]() ).
).
(1)为了使这种商品的生产费用平均每吨最低,那么这种商品的产量应为多少吨?
(2)如果生产出来的商品能全部卖完,当产量是120吨时企业利润最大,此时出售价格是每吨160万元,求![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,a1=2,且a1,a2,a3-2成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.

(1)求证:AE⊥B1C;
(2)若G为C1C中点,求二面角C-AG-E的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有下面四个命题:①底面是正多边形,其余各面都是等腰三角形的棱锥是正棱锥.②底面是正三角形,相邻两侧面所成二面角都相等的三棱锥是正三棱锥.③有两个面互相平行,其余四个面都是全等的等腰梯形的六面体是正四棱台.④有两个面互相平行,其余各个面是平行四边形的多面体是棱柱.其中,正确的命题的个数是( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,定义f1(x)=f(x),fn+1(x)=f[fn(x)](n∈N*),已知偶函数g(x)的定义域为(﹣∞,0)∪(0,+∞),g(1)=0,当x>0且x≠1时,g(x)=f2018(x).
,定义f1(x)=f(x),fn+1(x)=f[fn(x)](n∈N*),已知偶函数g(x)的定义域为(﹣∞,0)∪(0,+∞),g(1)=0,当x>0且x≠1时,g(x)=f2018(x).
(1)求f2(x),f3(x),f4(x),f2018(x);
(2)求出函数y=g(x)的解析式;
(3)若存在实数a、b(a<b),使得函数g(x)在[a,b]上的值域为[mb,ma],求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com