
【题目】已知![]() 的三个顶点都在椭圆C:
的三个顶点都在椭圆C:![]() 上,且
上,且![]() 过椭圆的左焦点F,O为坐标原点,M在
过椭圆的左焦点F,O为坐标原点,M在![]() 上,且
上,且![]() .
.
(1)求点M的轨迹方程;
(2)求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)
【解析】
(1)法一(代数法)设![]() :
:![]() ,
,![]() ,联立方程组,消去m得
,联立方程组,消去m得![]() ,即可推出结果.
,即可推出结果.
法二(几何法)由已知可得![]() ,
,![]() ,说明M的轨迹为以
,说明M的轨迹为以![]() 为直径的圆(经检验,原点也符合题意).求解即可.
为直径的圆(经检验,原点也符合题意).求解即可.
(2)由(1)知,M的轨迹为以![]() 为圆心,1为半径的圆,设
为圆心,1为半径的圆,设![]() ,则
,则![]() ,求出
,求出![]() 的表达式,利用二次函数的性质求解最大值与最小值即可.
的表达式,利用二次函数的性质求解最大值与最小值即可.
(1)法一(代数法)
由已知可得![]() ,故当直线
,故当直线![]() 斜率不为0时,可设
斜率不为0时,可设![]() :
:![]() ,
,![]()
由![]() 消去m得
消去m得![]() (
(![]() )
)
经检验,当直线![]() 斜率为0,即m存在时,
斜率为0,即m存在时,![]() 也符合上式,
也符合上式,
故点M的轨迹方程为:![]() .
.
法二(几何法)
由已知可得![]() ,
,![]() ,
,
所以M的轨迹为以![]() 为直径的圆(经检验,原点也符合题意),
为直径的圆(经检验,原点也符合题意),
∴M的轨迹方程为:![]() .
.
(2)由(1)知,M的轨迹为以![]() 为圆心,1为半径的圆,设
为圆心,1为半径的圆,设![]()
则![]() (
(![]() ),
),
可得 ,
,
当![]() 时,
时,
当![]() 时,
时,![]() ,
,
所以![]() 的取值范围是
的取值范围是 .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起,使得点
折起,使得点![]() 到点
到点![]() 位置,且
位置,且![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上的动点(与点
上的动点(与点![]() ,
,![]() 不重合).
不重合).
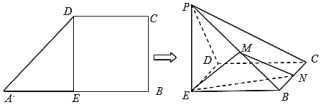
(Ⅰ)证明:平面![]() 平面
平面![]() 垂直;
垂直;
(Ⅱ)是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值
的余弦值![]() ?若存在,确定
?若存在,确定![]() 点位置;若不存在,说明理由.
点位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】维生素C又叫抗坏血酸,是一种水溶性维生素,是高等灵长类动物与其他少数生物的必需营养素.维生素C虽不直接构成脑组织,也不向脑提供活动能源,但维生素C有多种健脑强身的功效,它是脑功能极为重要的营养物.维生素C的毒性很小,但食用过多仍可产生一些不良反应.根据食物中维C的含量可大致分为:含量很丰富:鲜枣、沙棘、猕猴桃、柚子,每100克中的维生素C含量超过100毫克;比较丰富:青椒、桂圆、番茄、草莓、甘蓝、黄瓜、柑橘、菜花,每100克中维生素C含量超过50毫克;相对丰富:白菜、油菜、香菜、菠菜、芹菜、苋菜、菜苔、豌豆、豇豆、萝卜,每100克中维生素C含量超过30~50毫克.现从猕猴桃、柚子两种食物中测得每100克所含维生素C的量(单位:![]() )得到茎叶图如图所示,则下列说法中不正确的是( )
)得到茎叶图如图所示,则下列说法中不正确的是( )
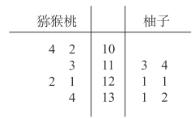
A.猕猴桃的平均数小于柚子的平均数
B.猕猴桃的方差小于柚子的方差
C.猕猴桃的极差为32
D.柚子的中位数为121
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设30多个分支机构,需要国内公司外派大量80后、90后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从80后和90后的员工中随机调查了100位,得到数据如下表:
愿意被外派 | 不愿意被外派 | 合计 | |
80后 | 20 | 20 | 40 |
90后 | 40 | 20 | 60 |
合计 | 60 | 40 | 100 |
(1)根据调查的数据,是否有99%的把握认为“是否愿意被外派与年龄有关”,并说明理由;
(2)该公司举行参观驻海外分支机构的交流体验活动,拟安排6名参与调查的80后、90后员工参加.80后员工中有愿意被外派的3人和不愿意被外派的3人报名参加,从中随机选出3人,记选到愿意被外派的人数为![]() ;90后员工中有愿意被外派的4人和不愿意被外派的2人报名参加,从中随机选出3人,记选到愿意被外派的人数为
;90后员工中有愿意被外派的4人和不愿意被外派的2人报名参加,从中随机选出3人,记选到愿意被外派的人数为![]() ,求
,求![]() 的概率.
的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式: ,其中
,其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,分别过
有且仅有一个公共点,分别过![]() 两点作
两点作![]() ,垂足分别为
,垂足分别为![]() ,且记
,且记![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离, ![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,![]() 为点
为点![]() 到点
到点![]() 的距离,试探索
的距离,试探索![]() 是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线的参数方程为
,直线的参数方程为![]() ,(
,(![]() 为参数).直线
为参数).直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程.
的普通方程.
(2)设![]() ,若
,若![]() 成等比数列,求
成等比数列,求![]() 和的
和的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 在
在![]() 轴上,
轴上,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,经过点
,经过点![]() 且垂直于
且垂直于![]() 轴的直线与抛物线
轴的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 到直线
到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com