
【题目】设p:实数x满足![]() ,其中
,其中![]() ,命题
,命题![]() 实数
实数![]() 满足
满足
|x-3|≤1 .
(1)若![]() 且
且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]()
![]() 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() 、
、![]() 。已知
。已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2。
,如图2。
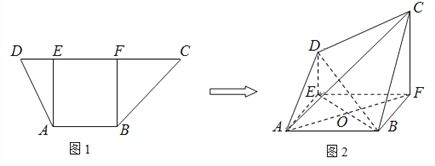
(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() ;
;
(3)在(1),(2)的条件下,求三棱锥![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,左、右焦点
的中心在坐标原点,左、右焦点![]() 分别在
分别在![]() 轴上,离心率为
轴上,离心率为![]() ,在其上有一动点
,在其上有一动点![]() ,
,![]() 到点
到点![]() 距离的最小值是1.过
距离的最小值是1.过![]() 作一个平行四边形,顶点
作一个平行四边形,顶点![]() 都在椭圆
都在椭圆![]() 上,如图所示.
上,如图所示.
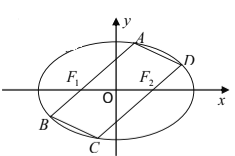
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)判断![]() 能否为菱形,并说明理由.
能否为菱形,并说明理由.
(Ⅲ)当![]() 的面积取到最大值时,判断
的面积取到最大值时,判断![]() 的形状,并求出其最大值.
的形状,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)是一个水平放置的正三棱柱![]() ,
, ![]() 是棱
是棱![]() 的中点,正三棱柱的主视图如图(2).
的中点,正三棱柱的主视图如图(2).
(1)图(1)中垂直于平面![]() 的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
(2)求正三棱柱![]() 的体积;
的体积;
(3)证明: ![]() 平面
平面![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年12月16日,科幻片《侠盗一号》上映,上映至今,全球累计票房高达8亿美金.为了了解娄底观众的满意度,某影院随机调查了本市观看影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
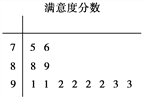
(1)求从这12人中随机选取1人,该人不是“满意观众”的概率;
(2)从本次所记录的满意度评分大于9.1的“满意观众”中随机抽取2人,求这2人得分不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五面体![]() 中,
中,![]() ,底面
,底面![]() 是正三角形,
是正三角形,![]() ,四边形
,四边形![]() 是矩形,二面角
是矩形,二面角![]() 为直二面角.
为直二面角.
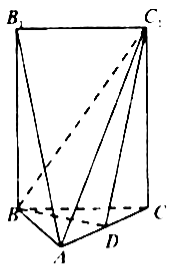
(1)![]() 在
在![]() 上运动,当
上运动,当![]() 在何处时,有
在何处时,有![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)当![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 余弦值.
余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com