
【题目】已知抛物线C:![]() ,点
,点![]() 在x轴的正半轴上,过点M的直线l与抛线C相交于A、B两点,O为坐标原点.
在x轴的正半轴上,过点M的直线l与抛线C相交于A、B两点,O为坐标原点.
![]() 若
若![]() ,且直线l的斜率为1,求证:以AB为直径的圆与抛物线C的准线相切;
,且直线l的斜率为1,求证:以AB为直径的圆与抛物线C的准线相切;
![]() 是否存在定点M,使得不论直线l绕点M如何转动,
是否存在定点M,使得不论直线l绕点M如何转动,![]() 恒为定值?若存在,请求出点M的坐标;若不存在,请说明理由.
恒为定值?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】(1)见证明;(2)见解析
【解析】
![]() 写出直线AB方程为
写出直线AB方程为![]() ,与抛物线方程联立,利用韦达定理与弦长公式计算
,与抛物线方程联立,利用韦达定理与弦长公式计算![]() 值,并求出线段AB的中点到准线的距离,证明该距离等于
值,并求出线段AB的中点到准线的距离,证明该距离等于![]() 的一半,即可证明结论成立;
的一半,即可证明结论成立;![]() 设直线AB的方程为
设直线AB的方程为![]() ,并设点
,并设点![]() 、
、![]() ,列出韦达定理,结合弦长公式得出
,列出韦达定理,结合弦长公式得出![]() 的表达式,根据表达式为定值得出m的值,从而可求出定点M的坐标.
的表达式,根据表达式为定值得出m的值,从而可求出定点M的坐标.
![]() 当
当![]() 时,且直线l的斜率为1时,直线l的方程为
时,且直线l的斜率为1时,直线l的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
将直线l的方程代入抛物线C的方程,消去y得,![]() ,
,
由韦达定理可得![]() ,
,![]() ,
,
由弦长公式可得![]() ,
,
线段AB的中点的横坐标为3,所以,线段AB的中点到抛物线准线![]() 的距离为4,
的距离为4,
因此,以AB为直径的圆与抛物线C的准线相切;
![]() 设直线l的方程为
设直线l的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
将直线l的方程代入抛物线方程并化简得![]() ,
,
由韦达定理可得![]() ,
,![]() ,
,
![]() ,同理可得
,同理可得![]() ,
,
所以, 为定值,
为定值,
所以,![]() ,即
,即![]() 时,
时,![]() 恒为定值
恒为定值![]() .
.
此时,定点M的坐标为![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x),对任意的a,b∈R,都有f(a+b)=f(a)+f(b)-1,并且当x<0时,f(x)>1.
(1)求证:f(x)是R上的减函数;
(2)若f(6)=7,解不等式f(3m2-2m-2)<4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3-
x3-![]() ax2,a∈R.
ax2,a∈R.
(1)当a=2时,求曲线y=f(x)在点(3,f(3))处的切线方程;
(2)设函数g(x)=f(x)+(x-a)cos x-sin x,讨论g(x)的单调性并判断有无极值,有极值时求出极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立70周年,也是全面建成小康社会的关键之年.为喜迎祖国70周年生日,全民齐心奋力建设小康社会,某校特举办“喜迎国庆,共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手的答题得分情况,则下列说法正确的是( )
甲 | 乙 | |||||
5 | 7 | 7 | ||||
7 | 3 | 2 | 8 | 3 | 4 | 5 |
3 | 9 | 1 | ||||
A.甲组选手得分的平均数小于乙组选手得分的平均数.
B.甲组选手得分的中位数大于乙组选手得分的平均数.
C.甲组选手得分的中位数等于乙组选手得分的中位数.
D.甲组选手得分的方差大于乙组选手得分的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段,某公路段的车流量![]() (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度![]() (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为:![]() .
.
(1)在该时段内,当汽车的平均速度![]() 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
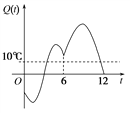
【题目】某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示,已知该年的平均气温为10 ℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-![]() ,0),B(
,0),B(![]() ,0),直线MA,MB交于点M,它们的斜率之积为常数m(m≠0),且△MAB的面积最大值为
,0),直线MA,MB交于点M,它们的斜率之积为常数m(m≠0),且△MAB的面积最大值为![]() ,设动点M的轨迹为曲线E.
,设动点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)过曲线E外一点Q作E的两条切线l1,l2,若它们的斜率之积为-1,那么![]() ·
·![]() 是否为定值?若是,请求出该值;若不是,请说明理由.
是否为定值?若是,请求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (k为常数,e=2.718 28…是自然对数的底数).
(k为常数,e=2.718 28…是自然对数的底数).
(1)当k≤0时,求函数f (x)的单调区间;
(2)若函数f (x)在(0,2)内存在两个极值点,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com