
Ζ÷Έω Θ®1Θ©ΗυΨίΧβ“βΘ§ΝΣΝΔ«σΫβΘ§«σ≥ωfΘ®tΘ©=xA•xB=$\frac{4t}{4t+1}$Θ§ΒΟ≥ωΫαΙϊΘΜ
Θ®2Θ©”…$\frac{1}{{a}_{n}}$=1+$\frac{1}{4{a}_{n-1}}$Θ§ΙΙ‘λ$\frac{1}{{a}_{n}}$+x=$\frac{1}{4}$Θ®$\frac{1}{{a}_{n-1}}$+xΘ©Θ§ΒΟ≥ω ΐΝ–{$\frac{1}{{a}_{n}}$-$\frac{4}{3}$}ΈΣq=$\frac{1}{4}$ΒΡΒ»±» ΐΝ–Θ§ ΉœνΈΣ$\frac{1}{a}$-$\frac{4}{3}$
Θ§¥”ΕχΒΟ≥ωaΒΡΖΕΈßΘΜ
Θ®3Θ©ΗυΨίΧβ“β«σ≥ωbn=$\frac{15}{4Θ®8•{4}^{n}-5Θ©}$Θ§άϊ”ΟΖ≈ΥθΖ®ΒΟ≥ωbnΘΨ$\frac{15}{2•{4}^{n+2}}$=$\frac{15}{32}•Θ®\frac{1}{4}Θ©^{n}$Θ§ΉνΚσΒΟ≥ωΫα¬έΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©ΓΏy-$\frac{1}{\sqrt{t}}$=$-\frac{1}{t}$Θ®x-$\sqrt{t}$Θ©”κy=4xœύΫΜ
ΓύxA=$\frac{2\sqrt{t}}{4t+1}$Θ§
Ννy=0ΒΟxB=2$\sqrt{t}$Θ§$\frac{1}{a}$
ΓύfΘ®tΘ©=xA•xB=$\frac{4t}{4t+1}$
Γύan=fΘ®an-1Θ©=$\frac{4{a}_{n-1}}{4{a}_{n-1}+1}$ΘΜ
Θ®2Θ©
ΓΏan=$\frac{4{a}_{n-1}}{4{a}_{n-1}+1}$Θ§
Γύ$\frac{1}{{a}_{n}}$=1+$\frac{1}{4{a}_{n-1}}$
…η$\frac{1}{{a}_{n}}$+x=$\frac{1}{4}$Θ®$\frac{1}{{a}_{n-1}}$+xΘ©Θ§
Γύ$\frac{1}{{a}_{n}}$=$\frac{1}{4{a}_{n-1}}$-$\frac{3}{4}x$Θ§
Γύx=$-\frac{4}{3}$Θ§
Γύ ΐΝ–{$\frac{1}{{a}_{n}}$-$\frac{4}{3}$}ΈΣq=$\frac{1}{4}$ΒΡΒ»±» ΐΝ–Θ§ ΉœνΈΣ$\frac{1}{a}$-$\frac{4}{3}$
Γύ Ι ΐΝ–{an}ΈΣΒίΦθ ΐΝ–Θ§«“ΈΣ’ΐ ΐ ΐΝ–{an}
Γύ$\frac{1}{a}$-$\frac{4}{3}$ΘΨ0Θ§
Γύ0ΘΦaΘΦ$\frac{3}{4}$ΘΜ
Θ®3Θ©”…Θ®2Θ©÷Σ ΐΝ–{$\frac{1}{{a}_{n}}$-$\frac{4}{3}$}ΈΣq=$\frac{1}{4}$ΒΡΒ»±» ΐΝ–Θ§ ΉœνΈΣ-$\frac{5}{6}$Θ§
Γύ$\frac{1}{{a}_{n}}$-$\frac{4}{3}$=-$\frac{5}{6}$ΓΝΘ®$\frac{1}{4}$Θ©n-1
Γύan=$\frac{6ΓΝ{4}^{n-1}}{8ΓΝ{4}^{n}-20}$Θ§
Γύbn=$\frac{15}{8ΓΝ{4}^{n}-20}$Θ§
ΓΏbnΘΨ$\frac{15}{8ΓΝ{4}^{n}}$=$\frac{15}{8}$ΓΝ$\frac{1}{{4}^{n}}$Θ§
${{s}_{n}}^{Γδ}$=$\frac{15}{8}$ΓΝ$\frac{1-\frac{1}{{4}^{n}}}{1-\frac{1}{4}}$=$\frac{5}{2}$-$\frac{5}{4}ΓΝ\frac{1}{{4}^{n}}$ΘΦ$\frac{3}{2}$Θ§
Γύ${S}_{nΘΦ}\frac{3}{2}$Θ°
ΒψΤά ΩΦ≤ιΝΥΚ· ΐΚΆ ΐΝ–ΒΡΉέΚœ”Π”ΟΚΆΖ≈ΥθΖ®ΒΡ”Π”ΟΘ§Ρ―Ε»Ϋœ¥σΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | a2ΘΦb2 | BΘ° | $\frac{1}{a}ΘΦ\frac{1}{b}$ | CΘ° | 2aΘΦ2b | DΘ° | abΘΦb2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 1 | BΘ° | 2 | CΘ° | 3 | DΘ° | 4 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ≥δΖ÷Εχ≤Μ±Ί“ΣΧθΦΰ | BΘ° | ±Ί“ΣΕχ≤Μ≥δΖ÷ΧθΦΰ | ||
| CΘ° | ≥δ“ΣΧθΦΰ | DΘ° | Φ»≤Μ≥δΖ÷“≤≤Μ±Ί“ΣΧθΦΰ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
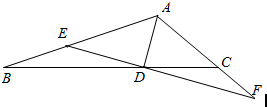 “―÷ΣΓςABC÷–Θ§AB=2Θ§AC=1Θ§ΓœBAC=120ΓψΘ§ADΈΣΫ«ΤΫΖ÷œΏΘ°
“―÷ΣΓςABC÷–Θ§AB=2Θ§AC=1Θ§ΓœBAC=120ΓψΘ§ADΈΣΫ«ΤΫΖ÷œΏΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | Θ®3Θ§5Θ© | BΘ° | [3Θ§5Θ© | CΘ° | Θ®1Θ§3Θ© | DΘ° | Θ®1Θ§3] |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com