
【题目】某市对大学生毕业后自主创业人员给予小额贷款补贴,贷款期限分为6个月、12个月、18个月、24个月、36个月五种,对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元,从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计,选取贷款期限的频数如表:
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率.
(Ⅰ)某大学2017年毕业生中共有3人准备申报此项贷款,计算其中恰有两人选择贷款期限为12个月的概率;
(Ⅱ)设给某享受此项政策的自主创业人员补贴为X元,写出X的分布列;该市政府要做预算,若预计2017年全市有600人申报此项贷款,则估计2017年该市共要补贴多少万元.
【答案】解:(Ⅰ)由题意知,每人选择贷款期限为12个月的概率为 ![]() , 所以3人中恰有2人选择此贷款的概率为
, 所以3人中恰有2人选择此贷款的概率为 ![]()
(Ⅱ)由题意知,享受补贴200元的概率为 ![]() ,享受补贴300元的概率为
,享受补贴300元的概率为 ![]() ,
,
享受补贴400元的概率为 ![]() ,即随机变量X的分布列为
,即随机变量X的分布列为
X | 200 | 300 | 400 |
P | | | |
∴ ![]() ,w=600×300=180000元.
,w=600×300=180000元.
所以,2017年政府需要补贴全市600人补贴款18万元
【解析】(Ⅰ)求出每人选择贷款期限为12个月的概率,然后利用独立重复试验概率的乘法求解3人中恰有2人选择此贷款的概率.(Ⅱ)求出享受补贴200元的概率为 ![]() ,享受补贴300元的概率为
,享受补贴300元的概率为 ![]() ,享受补贴400元的概率为
,享受补贴400元的概率为 ![]() ,即随机变量X的分布列,然后求解期望即可.
,即随机变量X的分布列,然后求解期望即可.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知长方形 ![]() ,
, ![]() ,
, ![]() ,以
,以 ![]() 的中点
的中点 ![]() 为原点,建立如图所示的平面直角坐标系
为原点,建立如图所示的平面直角坐标系 ![]() .
.
(1)求以 ![]() 为焦点,且过
为焦点,且过 ![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)在(1)的条件下,过点 ![]() 作直线
作直线 ![]() 与椭圆交于不同的两点
与椭圆交于不同的两点 ![]() ,设
,设 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,若
,若 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos2x﹣sin2x的图象向左平移 ![]() 个单位后得到函数F(x)的图象,则下列说法正确的是( )
个单位后得到函数F(x)的图象,则下列说法正确的是( )
A.函数F(x)是奇函数,最小值是 ![]()
B.函数F(x)是偶函数,最小值是 ![]()
C.函数F(x)是奇函数,最小值是﹣2
D.函数F(x)是偶函数,最小值是﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲参加A , B , C三个科目的学业水平考试,其考试成绩合格的概率如下表,假设三个科目的考试甲是否成绩合格相互独立.
科目A | 科目B | 科目C | |
甲 |
|
|
|
(I)求甲至少有一个科目考试成绩合格的概率;
(Ⅱ)设甲参加考试成绩合格的科目数量为X , 求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足① ![]() =
= ![]() ,②直线AQ与BP的交点在椭圆E:
,②直线AQ与BP的交点在椭圆E: ![]() +
+ ![]() =1(a>b>0)上.
=1(a>b>0)上.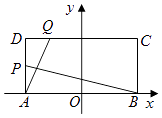
(Ⅰ)求椭圆E的方程;
(Ⅱ)设R为椭圆E的右顶点,M为椭圆E第一象限部分上一点,作MN垂直于y轴,垂足为N,求梯形ORMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个容量为M的样本数据,其频率分布表如下.
(1)计算a,b的值;
(2)画出频率分布直方图;
(3)用频率分布直方图,求出总体的众数及平均数的估计值.
频率分布表
分组 | 频数 | 频率 | 频率/组距 |
(10,20] | 2 | 0.10 | 0.010 |
(20,30] | 3 | 0.15 | 0.015 |
(30,40] | 4 | 0.20 | 0.020 |
(40,50] | a | b | 0.025 |
(50,60] | 4 | 0.20 | 0.020 |
(60, 70] | 2 | 0.10 | 0.010 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com