
����Ŀ��f��x���Ƕ�����D�ϵĺ���������������[m��n]D��ʹ����f��x����[m��n]�ϵ�ֵ��ǡΪ[km��kn]����ƺ���f��x����k�ͺ�������������˵������f��x��=3�� ![]() ��������k�ͺ����� ��������y=��
��������k�ͺ����� ��������y=�� ![]() x2+x��3�ͺ�������m=��4��n=0��
x2+x��3�ͺ�������m=��4��n=0��
���躯��f��x��=x3+2x2+x��x��0����k�ͺ�������k����СֵΪ ![]() ��
��
��������y= ![]() ��a��0����1�ͺ�������n��m�����ֵΪ
��a��0����1�ͺ�������n��m�����ֵΪ ![]() ��
��
����ѡ����ȷ���ǣ� ��
A.�٢�
B.�ڢ�
C.�ڢ�
D.�٢�
���𰸡�C
���������⣺���ڢ٣�f��x���Ķ�������{x|x��0}����f��2��=3�� ![]() =1��f��4��=3��
=1��f��4��=3�� ![]() =2�� ��f��x����[2��4]�ϵ�ֵ����[1��2]��f��x����
=2�� ��f��x����[2��4]�ϵ�ֵ����[1��2]��f��x���� ![]() �ͺ�����
�ͺ�����
��ٴ���
���ڢڣ�y=�� ![]() x2+x��3�ͺ���������
x2+x��3�ͺ��������� ![]() x2+x=3x�����x=0����x=��4����m=��4��n=0��
x2+x=3x�����x=0����x=��4����m=��4��n=0��
�����ȷ��
���ڢۣ�f��x��=x3+2x2+x��x��0����k�ͺ�������x3+2x2+x=kx�ж����ȸ�ʵ������
��x2+2x+��1��k��=0�ж����ȸ�ʵ������
�� ![]() �����0��k��1��
�����0��k��1��
��۴���
���ڢܣ�y= ![]() ��a��0����1�ͺ���������a2+a��x��1=a2x2 �� ��a2x2����a2+a��x+1=0��
��a��0����1�ͺ���������a2+a��x��1=a2x2 �� ��a2x2����a2+a��x+1=0��
��̵�����֮��x1��x2= ![]() =
= ![]() =
= ![]()
= ![]() ��
�� ![]() ����n��m�����ֵΪ
����n��m�����ֵΪ ![]() �������ȷ��
�������ȷ��
���ϣ���ȷ�������Ǣڢܣ�
��ѡ��C��
������Ŀ�е��¶��壬��Ϻ����뷽�̵�֪ʶ����һ�ж�����٢ڢۢ��Ƿ���ȷ���Ӷ�ȷ����ȷ�Ĵ𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() ������{an}��ǰn��ĺͼ�ΪSn ��
������{an}��ǰn��ĺͼ�ΪSn ��
��1����S1 �� S2 �� S3��ֵ������Sn�ı���ʽ��
��2��������ѧ���ɷ�֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����a1=1��Sn=2n��an��n��N*����
��1������a2 �� a3 �� a4 �� ���ɴ˲���ͨ�ʽan��
��2������ѧ���ɷ�֤����1���еIJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=ax2+��b��1��x+3��
��1��������ʽf��x����0�Ľ�Ϊ����1�� ![]() ������ʽbx2��3x+a��0�Ľ⼯��
������ʽbx2��3x+a��0�Ľ⼯��
��2����f��1��=4��a��0��b��0����ab�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ���װ��4����ȫ��ͬ��С�����Ϸֱ��������Ϊ0��1��2��2���ּ״�������һ������Żأ����ٴ�������һ�������������������ִ�ʤ����������ͬ��Ϊƽ�֣������ڼ�ʤ�������£�����1����ĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������һ����װ�У���ͼ��ʾ��ABCD�DZ߳�Ϊ60cm��������ӲֽƬ����ȥ��Ӱ������ʾ���ĸ�ȫ�ȵĵ���ֱ�������Σ�������������ʹ��A��B��C��D�ĸ����غ���ͼ�еĵ�P�������γ�һ������������״�İ�װ�У�E��F��AB�ϣ��DZ���ȥ�ĵ���ֱ��������б�ߵ������˵㣬��AE=FB=x��cm���� 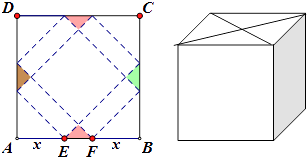
��1���������Ҫ���װ�в����S��cm2���������xӦȡ��ֵ��
��2���������Ҫ���װ���ݻ�V��cm3���������xӦȡ��ֵ���������ʱ��װ�еĸ������߳��ı�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=1+lnx�� ![]() ������kΪ������
������k������
��1����k=0��������y=f��x���ڵ㣨1��f��1�����������߷��̣�
��2����k=5����֤��f��x�����ҽ���������㣻
��3����kΪ�������ҵ�x��2ʱ��f��x����0���������k�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�A��B��C�������ε����ڽǣ�a��b��c�����ڽǶ�Ӧ�����ߣ���֪b2 �� a2 �� c2�ɵȲ����У�
��1����cosA����Сֵ��
��2����a=2����A���ʱ����ABC��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����g��x��=a��x2�� ![]() ��x��e��eΪ��Ȼ�����ĵ�������h��x��=2lnx��ͼ���ϴ��ڹ���x��ԳƵĵ㣬��ʵ��a��ȡֵ��Χ�ǣ� ��
��x��e��eΪ��Ȼ�����ĵ�������h��x��=2lnx��ͼ���ϴ��ڹ���x��ԳƵĵ㣬��ʵ��a��ȡֵ��Χ�ǣ� ��
A.[1�� ![]() +2]
+2]
B.[1��e2��2]
C.[ ![]() +2��e2��2]
+2��e2��2]
D.[e2��2��+�ޣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com