
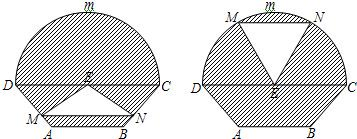
 如图所示的自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2a(a>
如图所示的自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2a(a>| 1 | 2 |
| 1 |
| 2 |
| MN-1 |
| 2a-1 |
| x | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
a2-(x-
|
| 1 |
| 2 |
| MN-1 |
| 2a-1 |
| x | ||
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
a2-(x-
|
| 1 |
| 2 |
a2-(x-
|
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| a-1 |
| 2(2a-1) |
| 1 |
| 2 |
| -a |
| 2(2a-1) |
| a-1 |
| 2(2a-1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| a-1 |
| 2(2a-1) |
| a-1 |
| 2(2a-1) |
| a2 |
| 4(2a-1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
a2-(x-
|
| 1 |
| 2 |
a2-(x-
|
| 1 |
| 2 |
(x-
|
(x-
| ||||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
| a2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
| a2 |
| 4(2a-1) |
| 4a-3 |
| 4(2a-1) |
| 1 |
| 2 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
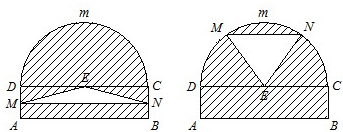 (2009•普陀区二模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).
(2009•普陀区二模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).查看答案和解析>>
科目:高中数学 来源: 题型:
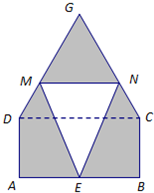 (2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.查看答案和解析>>
科目:高中数学 来源: 题型:
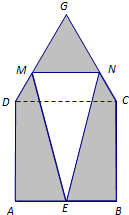 (2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海华师大一附中高三第二学期开学检测试题数学 题型:解答题
.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图所示的自动通风设施.该设施的下部 是等腰梯形,其中
是等腰梯形,其中 米,梯形的高为
米,梯形的高为 米,
米, 米,上部
米,上部 是个半圆,固定点
是个半圆,固定点 为
为 的中点.△
的中点.△ 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风), 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和 平行的伸缩横杆.
平行的伸缩横杆.
(1)设 与
与 之间的距离为
之间的距离为 米,试将三角通风窗
米,试将三角通风窗 的通风面积
的通风面积 (平方米)表示成关于
(平方米)表示成关于 的函数
的函数 ;
;
(2)当 与
与 之间的距离为多少米时,三角通风窗
之间的距离为多少米时,三角通风窗 的通风面积最大?并求出这个最大面积。
的通风面积最大?并求出这个最大面积。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com