
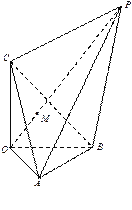
【题目】如图,已知三棱锥![]() 的三条侧棱
的三条侧棱![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直, ![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 内部一点,点
内部一点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】判断下列命题的真假:
(1)![]() 是
是![]() 的必要条件;
的必要条件;
(2)![]() 是
是![]() 的充要条件;
的充要条件;
(3)两个三角形的两组对应角相等是这两个三角形相似的充要条件;
(4)三角形的三条边满足勾股定理是这个三角形为直角三角形的充要条件;
(5)在![]() 中,重心和垂心重合是
中,重心和垂心重合是![]() 为等边三角形的必要条件;
为等边三角形的必要条件;
(6)如果点![]() 到点
到点![]() 的距离相等,则点
的距离相等,则点![]() 一定在线段
一定在线段![]() 的垂直平分线上.
的垂直平分线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,如图所示点
,如图所示点![]() 为椭圆上任意三点.
为椭圆上任意三点.

(Ⅰ)若![]() ,是否存在实数
,是否存在实数![]() ,使得代数式
,使得代数式![]() 为定值.若存在,求出实数
为定值.若存在,求出实数![]() 和
和![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅱ)若![]() ,求三角形
,求三角形![]() 面积的最大值;
面积的最大值;
(Ⅲ)满足(Ⅱ),且在三角形![]() 面积取得最大值的前提下,若线段
面积取得最大值的前提下,若线段![]() 与椭圆长轴和短轴交于点
与椭圆长轴和短轴交于点![]() (
(![]() 不是椭圆的顶点).判断四边形
不是椭圆的顶点).判断四边形![]() 的面积是否为定值.若是,求出定值;若不是,说明理由.
的面积是否为定值.若是,求出定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“冰桶挑战赛”是一项社交网络上发起的慈善公益活动,活动规定:被邀请者要么在![]() 小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外
小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外![]() 个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他![]() 个人发出邀请,则这
个人发出邀请,则这![]() 个人中至少有
个人中至少有![]() 个人接受挑战的概率是多少?
个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下列联表:

根据表中数据,能否有![]() %的把握认为“冰桶挑战赛与受邀者的性别有关”?
%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附: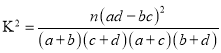

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术,通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍,若在正方形图案上随机取一点,则该点取自白色区域的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,点(an,an+1)在直线y=x+2上,且首项a1=1.
(1)求数列{an}的通项公式;
(2)数列{an}的前n项和为Sn,等比数列{bn}中,b1=a1,b2=a2,数列{bn}的前n项和为Tn,请写出适合条件Tn≤Sn的所有n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在各棱长均为2的三棱柱![]() 中,侧面
中,侧面![]() 底面ABC,
底面ABC,![]() .
.
(1)求侧棱![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知点D满足![]() ,在直线
,在直线![]() 上是否存在点P,使DP∥平面
上是否存在点P,使DP∥平面![]() ?若存在,请确定点P的位置,若不存在,请说明理由.
?若存在,请确定点P的位置,若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在x轴上且长轴长为4的椭圆C过点T(1,1),记l为圆O:x2+y2=1的切线
(1)求椭圆C的方程;
(2)若l与椭圆C交于A、B两点,求证:∠AOB为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com