
【题目】已知函数![]() .
.
(1)若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值
的最大值![]() ;
;
(2)在(1)成立的条件下,正实数![]() ,
,![]() 满足
满足![]() ,证明:
,证明:![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(2016·雅安高一检测)已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2),
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设桌面上有一个由铁丝围成的封闭曲线,周长是![]() .回答下面的问题:
.回答下面的问题:
(1)当封闭曲线为平行四边形时,用直径为![]() 的圆形纸片是否能完全覆盖这个平行四边形?请说明理由.
的圆形纸片是否能完全覆盖这个平行四边形?请说明理由.
(2)求证:当封闭曲线是四边形时,正方形的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工一件甲所需工时分别为1![]() ,2
,2![]() ,加工一件乙设备所需工时分别为2
,加工一件乙设备所需工时分别为2![]() ,1
,1![]() .A、B两种设备每月有效使用台时数分别为400
.A、B两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,分别用
,分别用![]() 表示计划每月生产甲,乙产品的件数.
表示计划每月生产甲,乙产品的件数.
(Ⅰ)用![]() 列出满足生产条件的数学关系式,并画出相应的平面区域;
列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种产品各多少件,可使收入最大?并求出最大收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列命题:
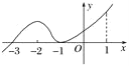
①-3是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在区间(-3,1)上单调递增;
④y=f(x)在x=0处切线的斜率小于零.
以上正确命题的序号是( )
A. ①②B. ③④C. ①③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com