
【题目】已知函数y=f(x)在定义域[-1,1]上既是奇函数,又是减函数.
(1)求证:对任意x1,x2∈[-1,1],有[f(x1)+f(x2)]·(x1+x2)≤0;
(2)若f(1-a)+f(1-a2)<0,求实数a的取值范围.
【答案】(1)见解析;(2)0≤a<1.
【解析】试题分析:(1)由x2∈[﹣1,1],可得﹣x2∈[﹣1,1],利用函数y=f(x)在定义域[﹣1,1]上是奇函数,又是减函数,即可证明结论;(2)f(1﹣a)+f(1﹣a2)<0,等价于a2+a﹣2<0,即可求出实数a的取值范围.
解析:
(1)证明:若x1+x2=0,显然不等式成立.
若x1+x2<0,则-1≤x1<-x2≤1,
因为f(x)在[-1,1]上是减函数且为奇函数,
所以f(x1)>f(-x2)=-f(x2),所以f(x1)+f(x2)>0.
所以[f(x1)+f(x2)](x1+x2)<0成立.
若x1+x2>0,则1≥x1>-x2≥-1,
同理可证f(x1)+f(x2)<0.
所以[f(x1)+f(x2)](x1+x2)<0成立.
综上得证,对任意x1,x2∈[-1,1],有[f(x1)+f(x2)]·(x1+x2)≤0恒成立.
(2)因为f(1-a)+f(1-a2)<0f(1-a2)<-f(1-a)=f(a-1),
所以由f(x)在定义域[-1,1]上是减函数,得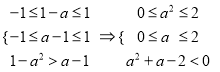
解得0≤a<1.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB的中点,且△PDB是正三角形,PA⊥PC.
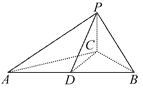
(1)求证:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在1798年,英国经济学家马尔萨斯(T.R.Malthus,1766—1834)就提出了自然状态下的人口增长模型: ![]() ,其中x表示经过的时间,
,其中x表示经过的时间, ![]() 表示x=0时的人口,r表示人口的平均增长率.
表示x=0时的人口,r表示人口的平均增长率.
下表是1950―1959年我国人口数据资料:

如果以各年人口增长率的平均值作为我国这一时期的人口增长率,用马尔萨斯人口增长模型建立我国这一时期的具体人口增长模型,某同学利用图形计算器进行了如下探究:
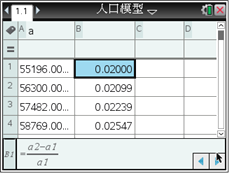
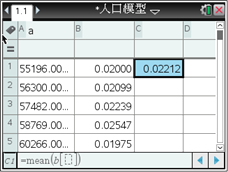
由此可得到我国1950―1959年我国这一时期的具体人口增长模型为____________. (精确到0.001)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=logax(a>0且a≠1)的图象过点(4,2),
(1)求a的值.
(2)若g(x)=f(1-x)+f(1+x),求g(x)的解析式及定义域.
(3)在(2)的条件下,求g(x)的单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:(x﹣1)2+y2= ![]() ,椭圆C:
,椭圆C: ![]() +y2=1,若直线l与椭圆交于A,B两点,与圆M相切于点P,且P为AB的中点,则这样的直线l有( )
+y2=1,若直线l与椭圆交于A,B两点,与圆M相切于点P,且P为AB的中点,则这样的直线l有( )
A.2条
B.3条
C.4条
D.6条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com