
【题目】设椭圆C:![]() (a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足
(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足![]() ,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
A.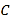 B.
B.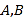
C.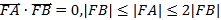 D.
D.![]()
【答案】A
【解析】
设椭圆左焦点为![]() ,由椭圆的对称性可知且
,由椭圆的对称性可知且![]() ,可得四边形AFBF′为矩形,设|AF′|=n,|AF|=m,根据椭圆的定义以及题意可知mn=2b2 ,从而可求得
,可得四边形AFBF′为矩形,设|AF′|=n,|AF|=m,根据椭圆的定义以及题意可知mn=2b2 ,从而可求得![]() 的范围,进而可求得离心率.
的范围,进而可求得离心率.
设椭圆左焦点为![]() ,由椭圆的对称性可知,四边形
,由椭圆的对称性可知,四边形![]() 为平行四边形,
为平行四边形,
又![]() ,即FA⊥FB,故平行四边形AFBF′为矩形,所以|AB|=|FF′|=2c.
,即FA⊥FB,故平行四边形AFBF′为矩形,所以|AB|=|FF′|=2c.
设|AF′|=n,|AF|=m,则在Rt△F′AF中,
m+n=2a ①,m2+n2=4c2 ②,
联立①②得mn=2b2 ③.
②÷③得![]() ,令
,令![]() =t,得t+
=t,得t+![]() .
.
又由|FB|≤|FA|≤2|FB|得![]() =t∈[1,2],所以t+
=t∈[1,2],所以t+![]() ∈
∈![]() .
.
故椭圆C的离心率的取值范围是 .
.
故选:A


科目:高中数学 来源: 题型:
【题目】某校进行了一次创新作文大赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在![]() 之间,其得分的频率分布直方图如图,则下列结论错误的是( )
之间,其得分的频率分布直方图如图,则下列结论错误的是( )
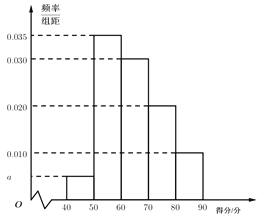
A.得分在![]() 之间的共有40人
之间的共有40人
B.从这100名参赛者中随机选取1人,其得分在![]() 的概率为0.5
的概率为0.5
C.估计得分的众数为55
D.这100名参赛者得分的中位数为65
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,且椭圆
,且椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合.过点
的焦点重合.过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆
过椭圆![]() 的上顶点,求
的上顶点,求![]() 的面积;
的面积;
(2)若![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于受到网络电商的冲击,某品牌的洗衣机在线下的销售受到影响,承受了一定的经济损失,现将![]() 地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
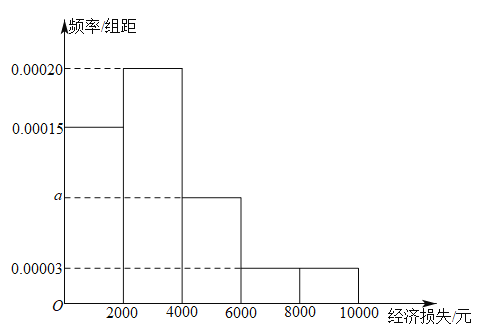
(1)求![]() 的值;
的值;
(2)求![]() 地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
(3)不经过计算,直接给出![]() 地区200家实体店经济损失的平均数
地区200家实体店经济损失的平均数![]() 与6000的大小关系.
与6000的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元2020年春,我国湖北武汉出现了新型冠状病毒,人感染后会出现发热、咳嗽、气促和呼吸困难等,严重的可导致肺炎甚至危及生命.为了尽快遏制住病毒的传播,我国科研人员,在研究新型冠状病毒某种疫苗的过程中,利用小白鼠进行科学试验.为了研究小白鼠连续接种疫苗后出现![]() 症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为
症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为![]() ,假设每次接种后当天是否出现
,假设每次接种后当天是否出现![]() 症状与上次接种无关.
症状与上次接种无关.
(1)若某只小白鼠出现![]() 症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
(2)若某只小白鼠在一个接种周期内出现2次或3次![]() 症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为
症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】10名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得2分,平局各得1分,负者得0分,并按总得分由高到低进行排序.比赛结束后,10名选手的得分各不相同,且第二名的得分是最后五名选手得分之和的![]() .则第二名选手的得分是____.
.则第二名选手的得分是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com