
����Ŀ��ijѧУΪ���������ѧ�����������������������ķ�����ȡ80��ѧ�����õ��������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��1������Ů�����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��2��������֪ͼ��1����������170��175cm������������16�ˣ�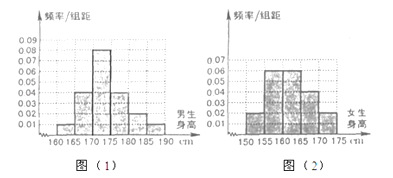
���������ڳ�ȡ��ѧ���У��С�Ů�����ж����ˣ�
������Ƶ�ʷֲ�ֱ��ͼ��������е�2��2�����������ж����ж�ٷּ����İ�����Ϊ���������Ա��йء���
��170cm | ��170cm | �ܼ� | |
�������� | |||
������ | |||
�ܼ� |
����������80��ѧ���У���������170��175cm֮���ѧ���а��С�Ů�Ա�ֲ�����ķ��������5�ˣ�����5����ѡ��3�˵����֣���3����ǡ����һ��Ů���ĸ��ʣ�
�ο���ʽ��K2=![]()
�ο����ݣ�
P��K2��k0�� | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡��⣺����ֱ��ͼ�У�
��������170��175cm��������Ƶ��Ϊ0.08��5=0.4��
��������Ϊn1 �� ��0.4=![]() ����n1=40��
����n1=40��
������������Ϊ40����Ů��������Ϊ80��40=40��
�����������ߡ�170cm������=��0.08+0.04+0.02+0.01����5��40=30��Ů�����ߡ�170cm������0.02��5��40=4�����Կɵõ�������������
��170cm | ��170cm | �ܼ� | |
�������� | 30 | 10 | 40 |
������ | 4 | 36 | 40 |
�ܼ� | 34 | 46 | 80 |
������99.9%�İ�����Ϊ�������Ա��йأ�
������170��175cm֮���������16�ˣ�Ů��������4�ˣ�
���ֲ�����ķ������5�ˣ�������ռ4�ˣ�Ů��ռ1�ˣ�
������ΪA1 �� A2 �� A3 �� A4 �� Ů��ΪB��
��5����ѡ3���У���A1 �� A2 �� A3������A1 �� A2 �� A4������A1 �� A2 �� B������A1 �� A3 �� A4������A1 �� A3 �� B������A1 �� A4 �� B������A2 �� A3 �� A4������A2 �� A3 �� B����
��A2 �� A4 �� B������A3 �� A4 �� B������10�ֿ��ܣ�
3����ǡ����һ��Ů���У���A1 �� A2 �� B������A1 �� A3 �� B������A1 �� A4 �� B������A2 �� A3 �� B������A2 �� A4 �� B������A3 �� A4 �� B������6�ֿ��ܣ�
���������Ϊ![]() ��
��
��������������ֱ��ͼ��������170��175cm��������Ƶ��Ϊ0.08��5=0.4���ɵ�������Ϊ40��������������Ϊ40����Ů��������Ϊ80��40=40��
��������������ߡ�170cm��������Ů�����ߡ�170cm���������õ�2��2�����������k2 �� ��𰸿���
���������170��175cm֮���������16�ˣ�Ů��������4�ˣ����ɷֲ�����ķ������5�ˣ��õ�����ռ4�ˣ�Ů��ռ1�ˣ�Ȼ������ö�ٷ��õ�ѡ��3�˵ķ������������3����ǡ����һ��Ů�������������ùŵ����ģ�ͼ��㹫ʽ�ô𰸣�
�����㾫����������Ҫ������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ�㣬��Ҫ����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ������ȷ�����⣮


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������C1��y2=4mx��m��0��������x�ύ��F1 �� ����ΪF2����F1 �� F2Ϊ���㣬������e=![]() ����ԲC2��������C1��x���Ϸ��Ľ���ΪP���ӳ�PF2���������ڵ�Q��M��������C1��һ���㣬��M��P��Q֮���˶���
����ԲC2��������C1��x���Ϸ��Ľ���ΪP���ӳ�PF2���������ڵ�Q��M��������C1��һ���㣬��M��P��Q֮���˶���
��m=1ʱ������ԲC2�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���о�ijҩƷ����Ч��ѡȡ������־Ը�߽����ٴ����飬����־Ը�ߵ�����ѹ���ݣ���λ��kPa���ķ�������Ϊ[12,13),[13,14),[14,15),[15,16),[16,17],���䰴�����ҵ�˳��ֱ���Ϊ��һ�飬�ڶ��飬![]() �������飬��ͼ�Ǹ������������Ƴɵ�Ƶ�ʷֲ�ֱ��ͼ����֪��һ����ڶ��鹲��20�ˣ���������û����Ч����6�ˣ��������������Ч������Ϊ�� ��
�������飬��ͼ�Ǹ������������Ƴɵ�Ƶ�ʷֲ�ֱ��ͼ����֪��һ����ڶ��鹲��20�ˣ���������û����Ч����6�ˣ��������������Ч������Ϊ�� ��
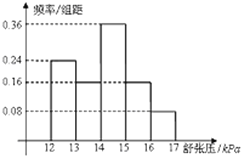
A. 6 B. 8 C. 12 D. 18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ʣ�0��+������
��1����a=6��b=5��c=4����ABC��BC��CA��AB�ij���֤����cosA��Q��
��2����a��b��c�ֱ�����ABC��BC��CA��AB�ij�����a��b��c��Qʱ��֤����cosA��Q��
��3�����������ʣ�-2��2������c2=a2+b2+��ab��֤����a��b��c������һ�������ε����߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=ax2+lnx��
����a=��1ʱ������y=f��x����ͼ���ڵ㣨1��f��1�����������߷��̣�
������֪a��0��������y=f��x����ͼ������ֱ��y=-![]() ���·�����a��ȡֵ��Χ��
���·�����a��ȡֵ��Χ��
����f�䣨x��Ϊ����f��x���ĵ���������a=1�����ʣ�������[1��10]���Ƿ����k��k��100��������x1 �� x2 �� x3��xk �� ʹ��f�䣨x1��+f�䣨x2��+f�䣨x3��+��+f�䣨xk����2012��������֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ǽ�����![]() ������ͼ��ֱ��ͼ.
������ͼ��ֱ��ͼ.

��1�����ж��߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ����˵�����ɣ�
����˵�����ɣ�
��2��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ������
������![]() ������
������![]() .
.
��1������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ������ʽ
ʱ������ʽ![]() ���������
���������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������C���ϰ���ԲC1�� ![]() =1��a��b��0��y��0���Ͳ���������C2��y=��x2+1��y��0�����Ӷ��ɣ�C1��C2�Ĺ�����ΪA��B������C1��������Ϊ
=1��a��b��0��y��0���Ͳ���������C2��y=��x2+1��y��0�����Ӷ��ɣ�C1��C2�Ĺ�����ΪA��B������C1��������Ϊ ![]() ��
�� 
��1����a��b��ֵ��
��2������B��ֱ��l��C1 �� C2�ֱ��ڵ�P��Q�������ڵ�A��B������AP��AQ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() �ϵ�������.��ʵ��
�ϵ�������.��ʵ��![]() ȡ���ֵʱ�������ڵ�
ȡ���ֵʱ�������ڵ�![]() ��ʹ�ù���
��ʹ�ù���![]() ��ֱ��������
��ֱ��������![]() Χ���������ͼ�Σ������������ͼ�ε��������ȣ����
Χ���������ͼ�Σ������������ͼ�ε��������ȣ����![]() ������Ϊ�� ��
�������� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com