
【题目】设函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 存在极值,对于任意的
存在极值,对于任意的![]() ,存在正实数
,存在正实数![]() ,使得
,使得![]() ,试判断
,试判断![]() 与
与![]() 的大小关系并给出证明.
的大小关系并给出证明.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )的图象在点
)的图象在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,且函数
,且函数![]() 为偶函数.若函数
为偶函数.若函数![]() 满足下列条件:①
满足下列条件:①![]() ;②对一切实数
;②对一切实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)求函数![]() 的表达式;
的表达式;
(2)设函数![]() (
(![]() )的两个极值点
)的两个极值点![]() ,
,![]() (
(![]() )恰为
)恰为![]() 的零点,当
的零点,当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋中装有2个白球和n(n≥2,n![]() N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
(I)用含n的代数式表示1次摸球中奖的概率;
(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;
(III)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 为坐标原点,动点
为坐标原点,动点![]() 满足:
满足:![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 都过点
都过点![]() ,且
,且![]() ,
,![]() 与轨迹
与轨迹![]() 分别交于点
分别交于点![]() ,试探究是否存在这样的直线?使得
,试探究是否存在这样的直线?使得![]() 是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
是等腰直角三角形.若存在,指出这样的直线共有几组(无需求出直线的方程);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家用电器公司生产一新款热水器,首先每年需要固定投入 200万元,其次每生产1百台,需再投入0.9万元.假设该公司生产的该款热水器当年能全部售出,但每销售1百台需另付运输费0.1万元.根据以往的经验,年销售总额![]() (万元)关于年产量
(万元)关于年产量![]() (百台)的函数为
(百台)的函数为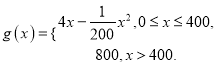 .
.
(1)将年利润![]() 表示为年产量
表示为年产量![]() 的函数;
的函数;
(2)求该公司生产的该款热水器的最大年利润及相应的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在![]() 天每件的销售价格
天每件的销售价格![]() (元)与时间
(元)与时间![]() (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (天)之间的关系如下表:
(天)之间的关系如下表:
|
|
|
|
|
|
|
|
|
|

(![]() )根据提供的图象(如图),写出该商品每件的销售价格
)根据提供的图象(如图),写出该商品每件的销售价格![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(![]() )根据表
)根据表![]() 提供的数据,写出日销售量
提供的数据,写出日销售量![]() 与时间
与时间![]() 的一次函数关系式.
的一次函数关系式.
(![]() )求该商品的日销售金额的最大值,并指出日销售金额最大的一天是
)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是![]() 天中的第几天.(日销售金额
天中的第几天.(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网时代的到来,手机的使用非常普遍,“低头族”随处可见。某校为了解家长和教师对学生带手机进校园的态度,随机调查了100位家长和教师,得到情况如下表:
教师 | 家长 | |
反对 | 40 | 20 |
支持 | 20 | 20 |
(1)是否有95%以上的把握认为“带手机进校园与身份有关”,并说明理由;
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附: 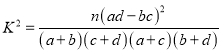
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高三学生的视力情况,随机地抽查了该校1000名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为![]() ,视力在4.6到5.0之间的学生数
,视力在4.6到5.0之间的学生数![]() ,
, ![]() 的值分别为( )
的值分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在“十一”黄金周期间降价搞促销,某超市对顾客实行购物优惠活动,规定一次购物付款总额:(1)如果不超过200元,则不予优惠;(2)如果超过200元,但不超过500元,则按标价给予9折优惠;(3)如果超过500元,其中500元按第(2)条给予优惠,超过500元的部分给予7折优惠。小张两次去购物,分别付款168元和423元,假设她一次性购买上述同样的商品,则应付款额为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com