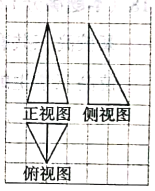
【题目】某几何体的三视图如图所示,网格纸上的小正方形边长为1,则此几何体的外接球的表面积为( )
A.
B.
C.
D.
【答案】B
【解析】
由三视图可还原得到三棱锥，三棱锥可放在如图底面边长为2，侧棱长为4的正四棱柱中，E，F为棱中点，设O为三棱锥外接球的球心，
分别为点Q在平面ABCD，平面ECD的投影.由于
都为等腰三角形，故分别在中线FG，EG上.构造直角三角形可求解得到
，结合
即得解.
由题设中的三视图，可得该几何体为如下图所示的三棱锥
，放在底面边长为2，侧棱长为4的正四棱柱中，E，F为棱中点，取G为CD中点，连接GF，GE.
设O为三棱锥外接球的球心，
分别为点O在平面ABCD，平面ECD的投影.由于都为等腰三角形，故分别在中线FG，EG上.
由于
，在
中，
设
；
同理在
中，
设
，
外接球半径
故外接球的表面积
故选：B
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，直线l的参数方程为
（t为参数），以O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ（ρ﹣2sinθ）＝1．
（1）求C的直角坐标方程；
（2）设直线l与y轴相交于P，与曲线C相交于A、B两点，且|PA|+|PB|＝2，求点O到直线l的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
的参数方程为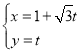
（
为参数），以坐标原点
为极点，
轴的非负半轴为极轴建立极坐标系，圆
的极坐标方程为
（1）求圆的圆心到直线的距离；
（2）己知
，若直线与圆交于
两点，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校为进行爱国主义教育，在全校组织了一次有关钓鱼岛历史知识的竞赛．现有甲、乙两队参加钓鱼岛知识竞赛，每队3人，规定每人回答一个问题，答对为本队赢得1分，答错得0分．假设甲队中每人答对的概率均为
，乙队中3人答对的概率分别为
，且各人回答正确与否相互之间没有影响，用ξ表示甲队的总得分．
（Ⅰ）求随机变量ξ的分布列和数学期望；
（Ⅱ）用
表示“甲、乙两个队总得分之和等于3”这一事件，用
表示“甲队总得分大于乙队总得分” 这一事件，求
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
(b为常数)
（1）若b=1,求函数H(x)=f(x)﹣g(x)图象在x=1处的切线方程;
（2）若b≥2,对任意x1,x2∈[1,2],且x1≠x2,都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求实数b的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图抛物线
的焦点为
，
为抛物线上一点（在
轴上方），
，点到
轴的距离为4.
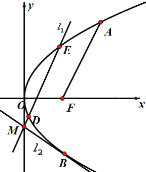
（1）求抛物线方程及点的坐标；
（2）是否存在轴上的一个点
，过点有两条直线
，满足
，
交抛物线
于
两点.
与抛物线相切于点
（不为坐标原点），有
成立，若存在，求出点的坐标.若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
