
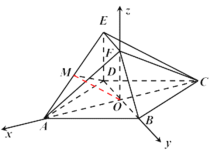
【题目】如图,在菱形![]() 中,
中,![]() ,平面
,平面![]() 平面
平面![]() 是线段
是线段![]() 的中点,
的中点,![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)设![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() ,则有
,则有![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,进而可证平面
,进而可证平面![]() 平面
平面![]() ,即可证明结论;
,即可证明结论;
(2)由已知![]() ,平面
,平面![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,连接
,连接![]() ,可证
,可证![]() 平面
平面![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,确定
为坐标原点建立空间直角坐标系,确定![]() 坐标,求出平面
坐标,求出平面![]() 的法向量,进而求出直线与平面所成角的正弦,再由三角函数关系,即可求出结论.
的法向量,进而求出直线与平面所成角的正弦,再由三角函数关系,即可求出结论.
(1)设![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() .
.
因为![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(2)因为![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
连接![]() ,则
,则![]() ,
,
故四边形![]() 是平行四边形,
是平行四边形,
故![]() ,从而
,从而![]() 平面
平面![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,
轴,
建立空间直角坐标系,则![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,令
,令![]() ,则
,则![]() ,
,
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
![]()
![]() ,
,
![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表.已知从全部210人中随机抽取1人为优秀的概率为![]() .
.
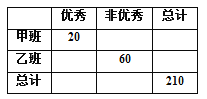
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(2)从全部210人中有放回地抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望E(ξ).
P(K2≥k0) | 0.05 | 0.01 |
k0 | 3.841 | 6.635 |
附: 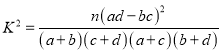
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校开设了射击选修课,规定向![]() 、
、![]() 两个靶进行射击:先向
两个靶进行射击:先向![]() 靶射击一次,命中得1分,没有命中得0分,向
靶射击一次,命中得1分,没有命中得0分,向![]() 靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向
靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,向
,向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
(1)求小明同学恰好命中一次的概率;
(2)求小明同学获得总分![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于独立性检验的叙述
①常用等高条形图表示列联表数据的频率特征;
②独立性检验依据小概率原理;
③独立性检验的结果是完全正确的;
④对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,
越小,![]() 与
与![]() 有关系的把握程度就越大.
有关系的把握程度就越大.
其中叙述正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知asinB=bsin(A![]() ).
).
(1)求A;
(2)D是线段BC上的点,若AD=BD=2,CD=3,求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com