
【题目】(本小题满分14分)
已知动点M到点![]() 的距离等于M到点
的距离等于M到点![]() 的距离的
的距离的![]() 倍.
倍.
(1)求动点M的轨迹C的方程;
(2)若直线![]() 与轨迹C没有交点,求
与轨迹C没有交点,求![]() 的取值范围;
的取值范围;
(3)已知圆![]() 与轨迹C相交于
与轨迹C相交于![]() 两点,求
两点,求![]()
【答案】(1) ![]()
(2)![]()
(3)![]()
【解析】
试题分析:注意把握求轨迹方程的四步曲,建系、设点、列式、化简,本题建系就省了,注意求哪个点的轨迹方程,就设哪个点的坐标为![]() ,根据题意,列出等量关系式,化简即可,对于第二问,注意考查的是圆与直线的位置关系,通过圆心到直线的距离与半径比较大小即可判断,对于第三问,涉及到两圆的公共弦长的问题,注意转化,将所求量放到相应的直角三角形中来求解.
,根据题意,列出等量关系式,化简即可,对于第二问,注意考查的是圆与直线的位置关系,通过圆心到直线的距离与半径比较大小即可判断,对于第三问,涉及到两圆的公共弦长的问题,注意转化,将所求量放到相应的直角三角形中来求解.
试题解析:
解:(1)设![]() ,则
,则![]() , (2分)
, (2分)
整理得![]() ,即动点M的轨迹C的方程为
,即动点M的轨迹C的方程为![]() . (4分)
. (4分)
(2)由 ,消去
,消去![]() 并化简得
并化简得![]() (6分)
(6分)
因为直线![]() 与轨迹C没有交点,所以
与轨迹C没有交点,所以![]() (8分)
(8分)
即![]() ,解得
,解得![]() . (9分)
. (9分)
(3)圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径
,半径![]() (10分)
(10分)
由 得
得![]() 这就是AB所在的直线方程, (11分)
这就是AB所在的直线方程, (11分)
又圆心![]() 到直线AB的距离
到直线AB的距离![]() , (13分)
, (13分)
所以![]() . (14分)
. (14分)
或:AB所在的直线方程![]() 与
与![]() 的交点坐标为
的交点坐标为![]() , (13分)
, (13分)
所以![]()


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】有甲、乙两种商品,经营销售这两种商品所得的利润依次为M万元和N万元,它们与投入资金![]() 万元的关系可由经验公式给出:M=
万元的关系可由经验公式给出:M=![]() ,N=
,N=![]() (
(![]() ≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,
≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,
设投入乙种商品的资金为![]() 万元,总利润
万元,总利润![]() ;
;
(2)为获得最大利润,对甲、乙两种商品的资金投入分别是多少?共能获得多大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·哈尔滨高二检测)如图,下列四个几何体中,它们的三视图(正视图、俯视图、侧视图)有且仅有两个相同,而另一个不同的两个几何体是________.


(1)棱长为2的正方体 (2)底面直径和高均为2的圆柱

(3)底面直径和高
均为2的圆锥
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设椭圆![]() 的离心率为
的离心率为![]() ,其左焦点
,其左焦点![]() 与抛物线
与抛物线![]() 的焦点相同.
的焦点相同.
(1)求此椭圆的方程;
(2)若过此椭圆的右焦点![]() 的直线
的直线![]() 与曲线
与曲线![]() 只有一个交点
只有一个交点![]() ,则
,则
①求直线![]() 的方程;
的方程;
②椭圆上是否存在点![]() ,使得
,使得![]() ,若存在,请说明一共有几个点;若不存在,请说明理由.
,若存在,请说明一共有几个点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
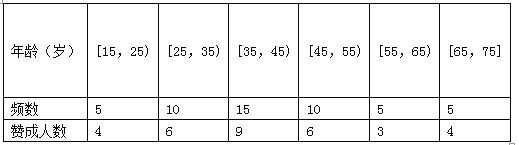
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,设函数
,设函数![]() .
.
(1)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)在(1)的条件下,当![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一数集的任一元素的倒数仍在该集合中,则称该数集为“可倒数集”.
(1)判断集合A={-1,1,2}是否为可倒数集;
(2)试写出一个含3个元素的可倒数集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com