
| AP |
| BP |
| 10 |
| 10 |
| AP |
| BP |
| AP |
| BP |
| 10 |
| AP |
| BP |
| 10 |
| 10 |


科目:高中数学 来源: 题型:
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市汶上一中高二12月质检理科数学试卷(带解析) 题型:填空题
点P(x,y)在圆C: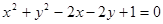 上运动,点A(-2,2),B(-2,-2)是平面上两点,则
上运动,点A(-2,2),B(-2,-2)是平面上两点,则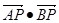 的最大值________.
的最大值________.
查看答案和解析>>
科目:高中数学 来源:2013年黑龙江省高三第四次联考理科数学试卷(解析版) 题型:解答题
已知直线 的参数方程为
的参数方程为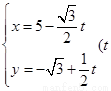 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
.
(I)判断直线 与圆C的位置关系;
与圆C的位置关系;
(Ⅱ)若点P(x,y)在圆C上,求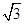 x +y的取值范围.
x +y的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届山东省济宁市高二12月质检理科数学试卷(解析版) 题型:填空题
点P(x,y)在圆C: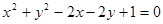 上运动,点A(-2,2),B(-2,-2)是平面上两点,则
上运动,点A(-2,2),B(-2,-2)是平面上两点,则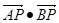 的最大值________.
的最大值________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com