
【题目】已知函数![]() ,函数
,函数![]() 的导函数
的导函数![]() ,且
,且![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求![]() 的极值;
的极值;
(Ⅱ)若存在![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,对于
时,对于![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】某电视台为了了解某社区居民对某娱乐节目的收视情况,随机抽取了![]() 名观众进行调查,下面是根据调查结果绘制的观众日均收看该娱乐节目时间的频率分布直方图:
名观众进行调查,下面是根据调查结果绘制的观众日均收看该娱乐节目时间的频率分布直方图:
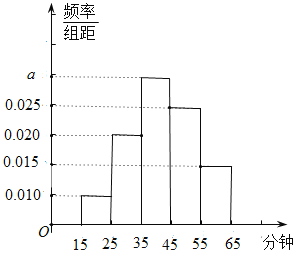
(1)求实数![]() 的值;
的值;
(2)根据统计结果,试估计观众观看该娱乐节目时间的中位数(结果保留一位小数);
(3)从观看时间在![]() ,
,![]() 的人中用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人的观看时间都在
的人中用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人的观看时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1-a≤x≤1+a}(a>0),B={x|x2-5x+4≤0}.
(1)若“x∈A”是“x∈B”的必要不充分条件,求实数a的取值范围;
(2)对任意x∈B,不等式x2-mx+4≥0都成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com