
【题目】已知椭圆C: ![]() ,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2. 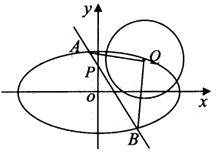
(1)求椭圆C的方程;
(2)过点P作直线l交椭圆C于A,B两点,若S△AQB=tan∠AQB,求直线l的方程.
【答案】
(1)解:因为椭圆C的右焦点F(c,0),|PF|=2,所以 ![]() ,
,
因为Q(2,1)在椭圆C上,所以 ![]() ,
,
由a2﹣b2=3,得a2=6,b2=3,
所以椭圆C的方程为 ![]()
(2)解:由S△AQB=tan∠AQB得: ![]() ,
,
即QAQBcos∠AQB=2,可得 ![]() ,
,
① 当l垂直x轴时, ![]()
![]() ,
,
此时满足题意,所以此时直线l的方程为x=0;
②当l不垂直x轴时,设直线l的方程为y=kx+1,
由 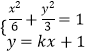 消去y得(1+2k2)x2+4kx﹣4=0,
消去y得(1+2k2)x2+4kx﹣4=0,
设A(x1,y1),B(x2,y2),所以 ![]() ,
, ![]() ,
,
代入 ![]() 可得:(x1﹣2,y1﹣1)(x2﹣2,y2﹣1)=2,
可得:(x1﹣2,y1﹣1)(x2﹣2,y2﹣1)=2,
代入y1=kx1+1,y2=kx2+1,得 ![]() ,
,
代入化简得: ![]() ,解得
,解得 ![]() ,
,
经检验满足题意,则直线l的方程为x﹣4y+4=0,
综上所述直线l的方程为x=0或x﹣4y+4=0
【解析】(1)由点P(0,1)到椭圆C的右焦点的距离为2PF|=2,可得c,由Q(2,1)在椭圆C上,得 ![]() ,及a2﹣b2=3,得a2 , b2 , (2)由S△AQB=tan∠AQB得:
,及a2﹣b2=3,得a2 , b2 , (2)由S△AQB=tan∠AQB得: ![]() ,即QAQBcos∠AQB=2,可得
,即QAQBcos∠AQB=2,可得 ![]() ,再联立直线与椭圆方程,由韦达定理可求解.
,再联立直线与椭圆方程,由韦达定理可求解.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(1)求圆C的极坐标方程;
(2)若直线l的极坐标方程是 ![]() ,射线
,射线 ![]() 与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (
( ![]() ),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小、材质都相同的![]() 个红球,
个红球,![]() 个黑球和
个黑球和![]() 个白球,从口袋中一次摸出一个球,连续摸球两次.
个白球,从口袋中一次摸出一个球,连续摸球两次.
(![]() )如果摸出后不放回,求第一次摸出黑球,第二次摸出白球的概率;
)如果摸出后不放回,求第一次摸出黑球,第二次摸出白球的概率;
(![]() )如果摸出后放回,求恰有一次摸到黑球的概率.
)如果摸出后放回,求恰有一次摸到黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两个企业的用电负荷量![]() 关于投产持续时间
关于投产持续时间![]() (单位:小时)的关系
(单位:小时)的关系![]() 均近似地满足函数
均近似地满足函数![]()
![]() .
.
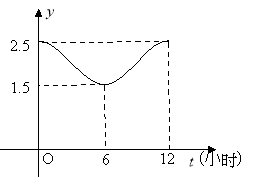
(1)根据图象,求函数![]() 的解析式;
的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过![]() ,现采用错峰用电的方式,让企业乙比企业甲推迟
,现采用错峰用电的方式,让企业乙比企业甲推迟![]()
![]() 小时投产,求
小时投产,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校期中考试数学试卷中,抽取样本,考察成绩分布,将样本分成5组,绘成频率分布直方图,图中各小组的长方形面积之比从左至右依次为1:3:6:4:2,第一组的频数是4.

(1)求样本容量及各组对应的频率;
(2)根据频率分布直方图估计成绩的平均分和中位数(结果保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣x﹣lnx,a∈R.
(1)当 ![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若﹣1≤a≤0,证明:函数f(x)有且只有一个零点;
(3)若函数f(x)有两个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,则实数m的取值范围是( )
,方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,则实数m的取值范围是( )
A.(﹣∞,﹣ ![]() )
)
B.(﹣ ![]() ,0)
,0)
C.(﹣ ![]() ,+∞)
,+∞)
D.(0, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com