
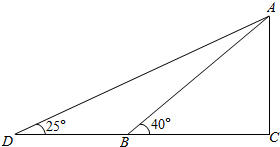
 如图所示,有一个堤坝,原斜坡AB长50m,坡角∠ABC=40°,现要将斜坡的坡角改成25°,即∠D=25°,那么斜坡的坡底要延长多少(精确到0.1m)?
如图所示,有一个堤坝,原斜坡AB长50m,坡角∠ABC=40°,现要将斜坡的坡角改成25°,即∠D=25°,那么斜坡的坡底要延长多少(精确到0.1m)? 分析 在△ABD中,∠BAD=40°-25°=15°.由正弦定理可得:$\frac{BD}{sin1{5}^{°}}$=$\frac{AB}{sin2{5}^{°}}$,即可得出.
解答 解:在△ABD中,∠BAD=40°-25°=15°.
由正弦定理可得:$\frac{BD}{sin1{5}^{°}}$=$\frac{AB}{sin2{5}^{°}}$,
∴$BD=\frac{50sin1{5}^{°}}{sin2{5}^{°}}$=$\frac{0.2588×50}{0.4226}$≈30.6.
答:斜坡的坡底要延长30.6m.
点评 本题考查了正弦定理的应用,考查了推理能力与计算能力,属于基础题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{c}$-($\overrightarrow{a}$+$\overrightarrow{b}$) | B. | $\overrightarrow{b}$-($\overrightarrow{a}+\overrightarrow{c}$) | C. | $\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | D. | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四面体ABCD中,△ABD,△ACD,△DBC和△ABC全等,且AB=AC=$\sqrt{3}$,BC=2;求证:平面BCD⊥平面ABC.
如图,在四面体ABCD中,△ABD,△ACD,△DBC和△ABC全等,且AB=AC=$\sqrt{3}$,BC=2;求证:平面BCD⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com