
【题目】已知函数f(x)![]() x+1,x∈R.
x+1,x∈R.
(1)求函数f(x)的最小正周期并写出函数f(x)图象的对称轴方程和对称中心;
(2)求函数f(x)在区间![]() 上的最大值和最小值.
上的最大值和最小值.
科目:高中数学 来源: 题型:
【题目】中央政府为了对应因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65的人群中随机调查50人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
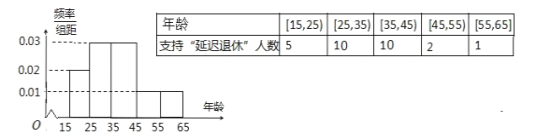
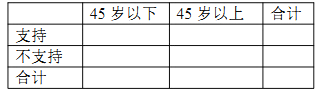
(1)由以上统计数据填下面2×2列联表,并问是否有90%的把握认为以45岁为分界点对“延迟退休年龄政策”的支持度有差异:
(2)若从年龄在![]() 的被调查人中随机选取两人进行调查,求选中的2人中恰有1人支持“延迟退休”的概率.
的被调查人中随机选取两人进行调查,求选中的2人中恰有1人支持“延迟退休”的概率.
参考数据:
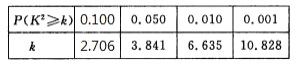
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左焦点为
)的左焦点为![]() ,其中四个顶点围成的四边形面积为
,其中四个顶点围成的四边形面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 的中点为
的中点为![]() ,
,![]() ,
,![]() 两点为椭圆
两点为椭圆![]() 上关于原点
上关于原点![]() 对称的两点,且
对称的两点,且![]() (
(![]() ),求四边形
),求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国文明城市,简称文明城市,是指在全面建设小康社会中市民整体素质和城市文明程度较高的城市.全国文明城市称号是反映中国大陆城市整体文明水平的最高荣誉称号.为普及相关知识,争创全国文明城市,某市组织了文明城市知识竞赛,现随机抽取了甲、乙两个单位各5名职工的成绩(单位:分)如下表:

(1)根据上表中的数据,分别求出甲、乙两个单位5名职工的成绩的平均数和方差,并比较哪个单位的职工对文明城市知识掌握得更好;
(2)用简单随机抽样法从乙单位5名职工中抽取2人,求抽取的2名职工的成绩差的绝对值不小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,以
,以![]() 为切点作函数
为切点作函数![]() 图象的切线交
图象的切线交![]() 轴于点
轴于点![]() ,再过
,再过![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,
,![]() ,以此类推得点
,以此类推得点![]() ,记
,记![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)证明数列![]() 为等比数列并求出通项公式;
为等比数列并求出通项公式;
(2)设直线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,记
,记![]() (其中
(其中![]() 为坐标原点),求数列
为坐标原点),求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数,
为参数,![]() ).
).
(1)若曲线![]() 与直线
与直线![]() 的一个交点纵坐标为
的一个交点纵坐标为![]() ,求
,求![]() 的值;
的值;
(2)若曲线![]() 上的点到直线
上的点到直线![]() 的最大距离为
的最大距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),得到如图5的茎叶图,整数位为茎,小数位为叶,如27.1mm的茎为27,叶为1.

(1)试比较甲、乙两种棉花的纤维长度的平均值的大小及方差的大小;(只需写出估计的结论,不需说明理由)
(2)将棉花按纤维长度的长短分成七个等级,分级标准如表:

试分别估计甲、乙两种棉花纤维长度等级为二级的概率;
(3)为进一步检验甲种棉花的其它质量指标,现从甲种棉花中随机抽取4根,记![]() 为抽取的棉花纤维长度为二级的根数,求
为抽取的棉花纤维长度为二级的根数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
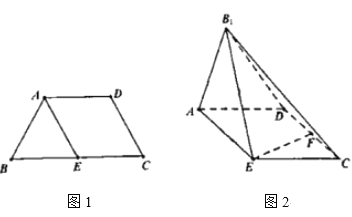
【题目】如图所示1,已知四边形ABCD满足![]() ,
,![]() ,E是BC的中点.将
,E是BC的中点.将![]() 沿着AE翻折成
沿着AE翻折成![]() ,使平面
,使平面![]() 平面AECD,F为CD的中点,如图所示2.
平面AECD,F为CD的中点,如图所示2.
(1)求证:![]() 平面
平面![]() ;
;
(2)求AE到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com