
分析 (I)根据函数奇偶性的,利用对称性求出函数f(x)的解析式,利用函数的单调性,结合函数的图象即可当x∈[-1,m](m>-1)时,求f(x)的值域;
(Ⅱ)根据函数值域,求出函数值对应的变量,结合函数的值域建立条件关系即可得到结论.
解答 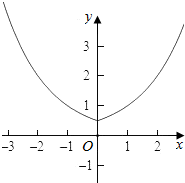 解:(I)若x<0,则-x>0,
解:(I)若x<0,则-x>0,
则f(-x)=2-x-1.
∵函数y=f(x)是偶函数,
∴f(-x)=2-x-1=f(x),
即f(x)=2-x-1,x<0.
当x=-1时,f(-1)=20=1,
当x≥0时,由f(x)=2x-1=1,得x-1=0,解得x=1,
当-1<m<0时,函数f(x)的最大值为f(-1)=1,最小值为f(m)=2-m-1,此时值域为[2-m-1,1],
当0≤m≤1时,函数f(x)的最大值为f(-1)=1,最小值为f(0)=$\frac{1}{2}$,此时值域为[$\frac{1}{2}$,1],
当m>1时,函数f(x)的最大值为f(m)=2m-1,最小值为f(0)=$\frac{1}{2}$,此时值域为[$\frac{1}{2}$,2m-1];
(Ⅱ)f(0)=$\frac{1}{2}$,由2x-1=2,得x-1=1,即x=2,由2-x-1=2,得-x-1=1,即x=-2,
若x∈[a,b],函数的值域为[$\frac{1}{2}$,2],
则0∈[a,b],且a=-2,或b=2,
若a=-2,则0≤b≤2,
若b=2,则-2≤a≤0.
点评 本题主要考查函数奇偶性的应用,以及函数值域的求解,利用函数图象结合函数单调性的性质是解决本题的关键.注意要进行分类讨论.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
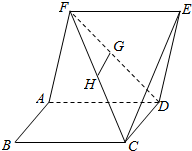 如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.
如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com