
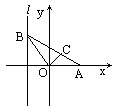
如图,给出定点A(a,0)(a>0)和直线l:x=-1,B是直线l上的一动点,∠BOA的平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.(注:文科题设还有条件a≠1).
|
本题主要考查曲线与方程、直线和圆锥曲线等基础知识以及求动点轨迹的基本技能和综合运用数学知识解决问题的能力. 解:依题可设B(-1,b)(b∈R), ∴直线OB方程为y=-bx,设点C(x,y),则0≤x<a. ∵OC平分∠AOB, ∴点C到OA、OB距离相等. ∴|y|= 又直线AB的方程为y=- ∴b= y2[1+ 整理得y2[(1-a)x2-2ax+(1+a)y2]=0. 当y≠0时,(1-a)x2-2ax+(1+a)y2=0.(0<x<a) 当y=0时,b=0,∠AOB=π,C(0,0)满足上式. ∴点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a). ∵a≠1, ∴方程可化为 ∴当0<a<1时,此方程表示椭圆的一部分. 当a>1时,此方程表示双曲线一支的一部分. |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
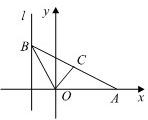 如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.查看答案和解析>>
科目:高中数学 来源: 题型:
如图,给出定点A(![]() , 0) (
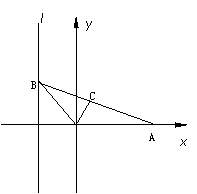
, 0) (![]() >0)和直线: x = 1 . B是直线l上的动点,ÐBOA的角平分线交AB于点C. 求点C的轨迹方程,并讨论方程表示的曲线类型与
>0)和直线: x = 1 . B是直线l上的动点,ÐBOA的角平分线交AB于点C. 求点C的轨迹方程,并讨论方程表示的曲线类型与![]() 值的关系.(14分)
值的关系.(14分)
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
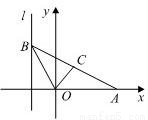
如图,给出定点A(a,0) (a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.

查看答案和解析>>
科目:高中数学 来源:1999年全国统一高考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com