
【题目】如图,在三棱锥![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.已知
的中点.已知![]() ,
,![]() .
.
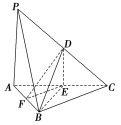
求证:(1)直线PA![]() 平面DEF;
平面DEF;
(2)平面BDE⊥平面ABC.
【答案】(1)见解析(2)见解析
【解析】
试题分析:(1) 由线面平行的判定定理可知,只须证PA与平面DEF内的某一条直线平行即可,由已知及图形可知应选择DE,由三角形的中位线的性质易知: DE∥PA ,从而问题得证;注意线PA在平面DEG外,而DE在平面DEF内必须写清楚;(2) 由面面垂直的判定定理可知,只须证两平中的某一直线与另一个平面垂直即可,注意题中已知了线段的长度,那就要注意利用勾股定理的逆定理来证明直线与直线的垂直;通过观察可知:应选择证DE垂直平面ABC较好,由(1)可知:DE⊥AC,再就只须证DE⊥EF即可;这样就能得到DE⊥平面ABC,又DE![]() 平面BDE,从面而有平面BDE⊥平面ABC.
平面BDE,从面而有平面BDE⊥平面ABC.
试题解析:(1)因为D,E分别为PC,AC的中点,所以DE∥PA.
又因为PA![]() 平面DEF,DE
平面DEF,DE![]() 平面DEF,所以直线PA∥平面DEF.
平面DEF,所以直线PA∥平面DEF.
(2)因为D,E,F分别人棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=![]() PA=3,EF=
PA=3,EF=![]() BC=4.
BC=4.
又因为DF=5,故DF2=DE2+EF2,所以∠DEF=90。,即DE⊥EF.又PA⊥AC,DE∥PA,所以DE⊥AC.
因为AC∩EF=E,AC![]() 平面ABC,EF
平面ABC,EF![]() 平面ABC,所以DE⊥平面ABC.
平面ABC,所以DE⊥平面ABC.
又DE![]() 平面BDE,所以平面BDE⊥平面ABC.
平面BDE,所以平面BDE⊥平面ABC.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.

(Ⅰ)求证:![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
(Ⅱ)求证:平面![]() ∥平面
∥平面![]() ;
;
(Ⅲ)画出平面![]() 与正方体侧面的交线(需要有必要的作图说明、保留作图痕迹).
与正方体侧面的交线(需要有必要的作图说明、保留作图痕迹).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 过点
过点![]() 和点
和点![]() .记两个圆的交点为
.记两个圆的交点为![]() 、
、![]() .
.
(1)如果直线![]() 的方程为
的方程为![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)当动圆![]() 的面积最小时,求两个圆心距离
的面积最小时,求两个圆心距离![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,规定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低![]() 元,根据市场调查,销售商一次订购不会超过600件.
元,根据市场调查,销售商一次订购不会超过600件.
(1)设一次订购![]() 件,服装的实际出厂单价为
件,服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com