
ЁОЬтФПЁПФГГЌЪаМЦЛЎАДдТЖЉЙКвЛжжвћСЯЃЌУПЬьНјЛѕСПЯрЭЌЃЌНјЛѕГЩБОУПЦП3дЊЃЌЪлМлУПЦП5дЊЃЌУПЬьЮДЪлГіЕФвћСЯзюКѓДђ4елЕБЬьШЋВПДІРэЭъ![]() ИљОнЭљФъЯњЪлОбщЃЌУПЬьашЧѓСПгыЕБЬьзюИпЦјЮТ
ИљОнЭљФъЯњЪлОбщЃЌУПЬьашЧѓСПгыЕБЬьзюИпЦјЮТ![]() ЕЅЮЛЃК
ЕЅЮЛЃК![]() гаЙи
гаЙи![]() ШчЙћзюИпЦјЮТВЛЕЭгк25ЃЌашЧѓСПЮЊ500ЦПЃЛШчЙћзюИпЦјЮТЮЛгкЧјМф
ШчЙћзюИпЦјЮТВЛЕЭгк25ЃЌашЧѓСПЮЊ500ЦПЃЛШчЙћзюИпЦјЮТЮЛгкЧјМф![]() ЃЌашЧѓСПЮЊ300ЦПЃЛШчЙћзюИпЦјЮТЕЭгк20ЃЌашЧѓСПЮЊ100ЦП
ЃЌашЧѓСПЮЊ300ЦПЃЛШчЙћзюИпЦјЮТЕЭгк20ЃЌашЧѓСПЮЊ100ЦП![]() ЮЊСЫШЗЖЈСљдТЗнЕФЖЉЙКМЦЛЎЃЌЭГМЦСЫЧАШ§ФъСљдТЗнИїЬьЕФзюИпЦјЮТЪ§ОнЃЌЕУЕНЯТУцЕФЦЕЪ§ЗжВМБэЃК
ЮЊСЫШЗЖЈСљдТЗнЕФЖЉЙКМЦЛЎЃЌЭГМЦСЫЧАШ§ФъСљдТЗнИїЬьЕФзюИпЦјЮТЪ§ОнЃЌЕУЕНЯТУцЕФЦЕЪ§ЗжВМБэЃК
зюИпЦјЮТ |
|
|
|
|
|
|
ЬьЪ§ | 2 | 16 | 36 | 25 | 7 | 4 |
вдзюИпЦјЮТЮЛгкИїЧјМфЕФЦЕТЪДњЬцзюИпЦјЮТЮЛгкИУЧјМфЕФИХТЪЃЎ
![]() Ђё
Ђё![]() ЧѓСљдТЗнетжжвћСЯвЛЬьЕФашЧѓСП
ЧѓСљдТЗнетжжвћСЯвЛЬьЕФашЧѓСП![]() ЕЅЮЛЃКЦП
ЕЅЮЛЃКЦП![]() ЕФЗжВМСаЃЌВЂЧѓГіЦкЭћEXЃЛ
ЕФЗжВМСаЃЌВЂЧѓГіЦкЭћEXЃЛ
![]() Ђђ
Ђђ![]() ЩшСљдТЗнвЛЬьЯњЪлетжжвћСЯЕФРћШѓЮЊ
ЩшСљдТЗнвЛЬьЯњЪлетжжвћСЯЕФРћШѓЮЊ![]() ЕЅЮЛЃКдЊ
ЕЅЮЛЃКдЊ![]() ЃЌЧвСљдТЗнетжжвћСЯвЛЬьЕФНјЛѕСПЮЊ
ЃЌЧвСљдТЗнетжжвћСЯвЛЬьЕФНјЛѕСПЮЊ![]() ЕЅЮЛЃКЦП
ЕЅЮЛЃКЦП![]() ЃЌЧыХаЖЯYЕФЪ§бЇЦкЭћЪЧЗёдк
ЃЌЧыХаЖЯYЕФЪ§бЇЦкЭћЪЧЗёдк![]() ЪБШЁЕУзюДѓжЕЃП
ЪБШЁЕУзюДѓжЕЃП
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁП
![]() Ђё
Ђё![]() гЩЬтвтжЊXЕФПЩФмШЁжЕЮЊ100ЃЌ300ЃЌ500ЃЌЗжБ№ЧѓГіЯргІЕФИХТЪЃЌгЩДЫФмЧѓГіXЕФЗжВМСаКЭ
гЩЬтвтжЊXЕФПЩФмШЁжЕЮЊ100ЃЌ300ЃЌ500ЃЌЗжБ№ЧѓГіЯргІЕФИХТЪЃЌгЩДЫФмЧѓГіXЕФЗжВМСаКЭ![]() ЃЎ
ЃЎ![]() Ђђ
Ђђ![]() СљдТЗнетжжвћСЯЕФНјЛѕСПnЃЌЕБ
СљдТЗнетжжвћСЯЕФНјЛѕСПnЃЌЕБ![]() ЪБЃЌЧѓГі
ЪБЃЌЧѓГі![]() ЃЌЙЪЕБ
ЃЌЙЪЕБ![]() ЪБЃЌYЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ520дЊЃЛЕБ
ЪБЃЌYЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ520дЊЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЙЪЕБ
ЃЌЙЪЕБ![]() ЪБЃЌYЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ480дЊ
ЪБЃЌYЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ480дЊ![]() гЩДЫФмЧѓГі
гЩДЫФмЧѓГі![]() ЪБЃЌyЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ520дЊЃЎ
ЪБЃЌyЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ520дЊЃЎ
НтЃК![]() Ђё
Ђё![]() гЩЬтвтжЊXЕФПЩФмШЁжЕЮЊ100ЃЌ300ЃЌ500ЃЌ
гЩЬтвтжЊXЕФПЩФмШЁжЕЮЊ100ЃЌ300ЃЌ500ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
X | 100 | 300 | 500 |
P |
|
|
|
![]() ЃЎ
ЃЎ
![]() Ђђ
Ђђ![]() гЩЬтвтжЊСљдТЗнетжжвћСЯЕФНјЛѕСПnТњзу
гЩЬтвтжЊСљдТЗнетжжвћСЯЕФНјЛѕСПnТњзу![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ
ШєзюИпЦјЮТВЛЕЭгк25ЃЌдђ![]() ЃЌ
ЃЌ
ШєзюИпЦјЮТЮЛгк![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ШєзюИпЦјЮТЕЭгк20ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ДЫЪБЃЌ![]() ЪБЃЌYЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ520дЊЃЌ
ЪБЃЌYЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ520дЊЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ
ШєзюИпЦјЮТВЛЕЭгк25ЃЌдђ![]() ЃЌ
ЃЌ
ШєзюИпЦјЮТЮЛгк![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ШєзюИпЦјЮТЕЭгк20ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ДЫЪБЃЌ![]() ЪБЃЌYЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ480дЊЃЌ
ЪБЃЌYЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ480дЊЃЌ
![]() ЪБЃЌYЕФЪ§бЇЦкЭћжЕЮЊЃК
ЪБЃЌYЕФЪ§бЇЦкЭћжЕЮЊЃК![]() ВЛЪЧзюДѓжЕЃЌ
ВЛЪЧзюДѓжЕЃЌ
![]() ЪБЃЌyЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ520дЊЃЎ
ЪБЃЌyЕФЪ§бЇЦкЭћДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ520дЊЃЎ


 бЇЯАЪЕМљдАЕиЯЕСаД№АИ
бЇЯАЪЕМљдАЕиЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпlЃК![]() Й§ХзЮяЯпCЃК
Й§ХзЮяЯпCЃК![]() ЕФНЙЕуFЃЌЧвгыХзЮяЯпCНЛгкЕуAЁЂBСНЕуЃЌЙ§AЁЂBСНЕуЗжБ№зїХзЮяЯпзМЯпЕФДЙЯпЃЌДЙзуЗжБ№ЮЊMЁЂNЃЌдђЯТСаЫЕЗЈДэЮѓЕФЪЧ
ЕФНЙЕуFЃЌЧвгыХзЮяЯпCНЛгкЕуAЁЂBСНЕуЃЌЙ§AЁЂBСНЕуЗжБ№зїХзЮяЯпзМЯпЕФДЙЯпЃЌДЙзуЗжБ№ЮЊMЁЂNЃЌдђЯТСаЫЕЗЈДэЮѓЕФЪЧ![]() ЁЁЁЁ
ЁЁЁЁ![]()
A. ХзЮяЯпЕФЗНГЬЮЊ![]() B. ЯпЖЮABЕФГЄЖШЮЊ
B. ЯпЖЮABЕФГЄЖШЮЊ![]()
C. ![]() D. ЯпЖЮABЕФжаЕуЕНyжсЕФОрРыЮЊ
D. ЯпЖЮABЕФжаЕуЕНyжсЕФОрРыЮЊ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃгУМђЕЅЫцЛњГщбљЗНЗЈГщШЁСЫ30УћЭЌбЇЃЌЖдЦфУПдТЦНОљПЮЭтдФЖСЪБМфЃЈЕЅЮЛЃКаЁЪБЃЉНјааЕїВщЃЌОЅвЖЭМШчЭМЃК
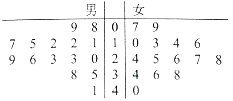
ШєНЋдТОљПЮЭтдФЖСЪБМфВЛЕЭгк30аЁЪБЕФбЇЩњГЦЮЊЁАЖСЪщУдЁБ.
ЃЈ1ЃЉНЋЦЕТЪЪгЮЊИХТЪЃЌЙРМЦИУаЃ900УћбЇЩњжаЁАЖСЪщУдЁБгаЖрЩйШЫЃП
ЃЈ2ЃЉДгвбГщШЁЕФ7УћЁАЖСЪщУдЁБжаЫцЛњГщШЁФаЁЂХЎЁАЖСЪщУдЁБИї1ШЫЃЌВЮМгЖСЪщШеаћДЋЛюЖЏ.
ЃЈiЃЉЙВгаЖрЩйжжВЛЭЌЕФГщШЁЗНЗЈЃП
ЃЈiiЃЉЧѓГщШЁЕФФаЁЂХЎСНЮЛЁАЖСЪщУдЁБдТОљЖСЪщЪБМфЯрВюВЛГЌЙ§2аЁЪБЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§![]() дкЦфЖЈвхгђЩЯЧЁгаСНИіСуЕуЃЌдђе§ЪЕЪ§aЕФжЕЮЊ_____.
дкЦфЖЈвхгђЩЯЧЁгаСНИіСуЕуЃЌдђе§ЪЕЪ§aЕФжЕЮЊ_____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() ЪЧздШЛЪ§ЕФЕзЪ§ЃЌ
ЪЧздШЛЪ§ЕФЕзЪ§ЃЌ![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌНтВЛЕШЪН
ЪБЃЌНтВЛЕШЪН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() дк
дк![]() ЩЯЪЧЕЅЕїдіКЏЪ§ЃЌЧѓ
ЩЯЪЧЕЅЕїдіКЏЪ§ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓећЪ§
ЪБЃЌЧѓећЪ§![]() ЕФЫљгажЕЃЌЪЙЗНГЬ
ЕФЫљгажЕЃЌЪЙЗНГЬ![]() дк
дк![]() ЩЯгаНт.
ЩЯгаНт.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§ ЃЌдђКЏЪ§gЃЈxЃЉЃНxfЃЈxЃЉЉ1ЕФСуЕуЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
ЃЌдђКЏЪ§gЃЈxЃЉЃНxfЃЈxЃЉЉ1ЕФСуЕуЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
A. 2B. 3C. 4D. 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчзгПЦММЙЋЫОгЩгкВњЦЗВЩгУзюаТММЪѕЃЌЯњЪлЖюВЛЖЯдіГЄЃЌзюНќ![]() ИіМОЖШЕФЯњЪлЖюЪ§ОнЭГМЦШчЯТБэЃЈЦфжа
ИіМОЖШЕФЯњЪлЖюЪ§ОнЭГМЦШчЯТБэЃЈЦфжа![]() БэЪО
БэЪО![]() ФъЕквЛМОЖШЃЌвдДЫРрЭЦЃЉЃК
ФъЕквЛМОЖШЃЌвдДЫРрЭЦЃЉЃК
МОЖШ |
|
|
|
|
|
МОЖШБрКХx |
|
|
|
|
|
ЯњЪлЖюyЃЈАйЭђдЊЃЉ |
|
|
|
|
|
ЃЈ1ЃЉЙЋЫОЪаГЁВПДгжаШЮбЁ![]() ИіМОЖШЕФЪ§ОнНјааЖдБШЗжЮіЃЌЧѓет
ИіМОЖШЕФЪ§ОнНјааЖдБШЗжЮіЃЌЧѓет![]() ИіМОЖШЕФЯњЪлЖюЖМГЌЙ§
ИіМОЖШЕФЯњЪлЖюЖМГЌЙ§![]() ЧЇЭђдЊЕФИХТЪЃЛ
ЧЇЭђдЊЕФИХТЪЃЛ
ЃЈ2ЃЉЧѓ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЃЌВЂдЄВтИУЙЋЫО
ЕФЯпадЛиЙщЗНГЬЃЌВЂдЄВтИУЙЋЫО![]() ЕФЯњЪлЖю.
ЕФЯњЪлЖю.
ИНЃКЯпадЛиЙщЗНГЬЃК![]() Цфжа
Цфжа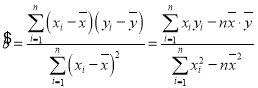 ЃЌ
ЃЌ![]()
ВЮПМЪ§ОнЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃЌЕу
ЃЌЕу![]() гыХзЮяЯп
гыХзЮяЯп![]() ЕФНЙЕу
ЕФНЙЕу![]() ЙигкдЕуЖдГЦЃЌЖЏЕу
ЙигкдЕуЖдГЦЃЌЖЏЕу![]() ЕНЕу
ЕНЕу![]() ЕФОрРыгыЕНЕу
ЕФОрРыгыЕНЕу![]() ЕФОрРыжЎКЭЮЊ4.
ЕФОрРыжЎКЭЮЊ4.
ЃЈ1ЃЉЧѓЖЏЕу![]() ЕФЙьМЃЃЛ
ЕФЙьМЃЃЛ
ЃЈ2ЃЉШє![]() ЃЌЩшЙ§Еу
ЃЌЩшЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гы
гы![]() ЕФЙьМЃЯрНЛгк
ЕФЙьМЃЯрНЛгк![]() СНЕуЃЌЕБ
СНЕуЃЌЕБ![]() ЕФУцЛ§зюДѓЪБЃЌЧѓжБЯп
ЕФУцЛ§зюДѓЪБЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌШє
ЃЌШє![]() ДцдкЮЈвЛЕФСуЕу
ДцдкЮЈвЛЕФСуЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌдђ
ЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com