练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对于个黑球和个白球的任意排列（从左到右排成一行），则一定（　　）

    A. 存在一个白球，它右侧的白球和黑球一样多

    B. 存在一个黑球，它右侧的白球和黑球一样多

    C. 存在一个白球，它右侧的白球比黑球少一个

    D. 存在一个黑球，它右侧的白球比黑球少一个

    【答案】B

    【解析】为奇数， 为偶数，故总存在一个黑球，它右侧的白球和黑球一样多．

    使用排除法：当100个黑球都排在右侧时，每一个白球右侧都有100个黑球，最左侧的白球的右侧的白球最多且有98个白球，所以不存在这样的白球使得它右侧的白球和黑球一样多，A不对；也不存在这样的白球使得它右侧的白球比黑球少一个，C不对；当最右侧排1个黑球，其余黑球在最左侧时，不存在这样的黑球使得它右侧的白球比黑球少一个，D不对．99为奇数，100为偶数，故总存在一个黑球，它右侧的白球和黑球一样多.

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】(1)关于的不等式的解集不是空集，求的取值范围；

    (2)设，，，且，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣4x+3，g（x）=m（x﹣1）+2（m＞0），若存在x1∈[0，3]，使得对任意的x2∈[0，3]，都有f（x1）=g（x2），则实数m的取值范围是（ ）
    A.
    B.（0，3]
    C.
    D.[3，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线f（x）= （x＞0）上有一点列Pn（xn ， yn）（n∈N*），过点Pn在x轴上的射影是Qn（xn ， 0），且x1+x2+x3+…+xn=2n+1﹣n﹣2．（n∈N*）
    （1）求数列{xn}的通项公式；
    （2）设四边形PnQnQn+1Pn+1的面积是Sn ， 求Sn；
    （3）在（2）条件下，求证： + +…+ ＜4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对一批产品的长度（单位：mm）进行抽样检测，下图为检测结果的频率分布直方图．根据标准，产品长度在区间[20，25）上的为一等品，在区间[15，20）和区间[25，30）上的为二等品，在区间[10，15）和[30，35）上的为三等品．用频率估计概率，现从该批产品中随机抽取一件，则其为二等品的概率为（ ）
    A.0.09
    B.0.20
    C.0.25
    D.0.45

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线y2=4x，点M（1，0）关于y轴的对称点为N，直线l过点M交抛物线于A，B两点．
    （1）证明：直线NA，NB的斜率互为相反数；
    （2）求△ANB面积的最小值；
    （3）当点M的坐标为（m，0），（m＞0且m≠1）．根据（1）（2）推测：△ABC面积的最小值是多少？（不必说明理由）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，锐角α和钝角β的终边分别与单位圆交于A，B两点．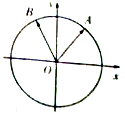
    （I）若A，B两点的纵会标分别为 的值；
    （II）已知点C是单位圆上的一点，且 的夹角θ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ ）的部分图象如图所示，下列说法正确的是（ ）
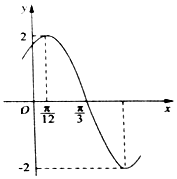
    A.函数f（x）的图象关于直线x=﹣ 对称
    B.函数f（x）的图象关于点（﹣ ，0）对称
    C.若方程f（x）=m在[﹣ ，0]上有两个不相等的实数根，则实数m∈（﹣2，﹣ ]
    D.将函数f（x）的图象向左平移 个单位可得到一个偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若，且，则的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案