
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是等边三角形,且侧面
是等边三角形,且侧面![]() 底面
底面![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
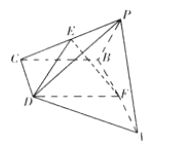
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)连接![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,
, ![]() ,得到四边形
,得到四边形![]() 是平行四边形,∴
是平行四边形,∴![]() 为
为![]() 的中点.由
的中点.由![]() 为
为![]() 的中点,可得
的中点,可得![]() ,从而证明
,从而证明![]() 平面
平面![]() .
.
(Ⅱ)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示坐标系,
轴建立如图所示坐标系,
利用向量法能求出平面![]() 与平面
与平面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
试题解析:(Ⅰ)连接![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,
, ![]() ,
,
∵![]() 且
且![]() ,
, ![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
, ![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() 为
为![]() 的中点.
的中点.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)连接![]() ,∵
,∵![]() 为
为![]() 的边
的边![]() 的中点,∴
的中点,∴![]() ,
,
∵平面![]() 底面
底面![]() ,∴
,∴![]() 底面
底面![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示坐标系,
轴建立如图所示坐标系,

设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 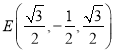 ,
,
∴![]() ,
, 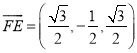 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则 .即
.即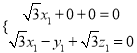 ,
,
令![]() ,得
,得![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则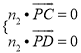 .即
.即 ,
,
令![]() ,得
,得![]() ,
,
设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() (锐角),
(锐角),
则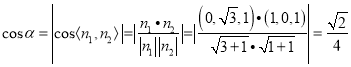 .
.
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在[﹣1,1]上的奇函数f(x),已知当x∈[﹣1,0]时的解析式f(x)= ![]() ﹣
﹣ ![]() (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一个居民月用电量标准![]() ,用电量不超过
,用电量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以
的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
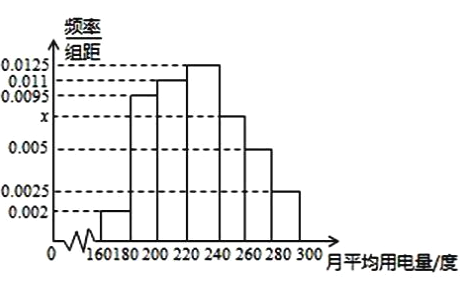
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)如果当地政府希望使![]() 左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准
左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准![]() 应该定为多少合理?
应该定为多少合理?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3万元、2万元,甲、乙产品都需要在![]() 两种设备上加工,在每台
两种设备上加工,在每台![]() 上加工1件甲所需工时分别是1
上加工1件甲所需工时分别是1![]() 、2
、2![]() ,加工1件乙所需工时分别为2
,加工1件乙所需工时分别为2![]() 、1
、1![]() ,
, ![]() 两种设备每月有效使用台时数分别为400
两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,如何安排生产可使收入最大?
,如何安排生产可使收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,(a>0).
,(a>0).
(1)当a=2时,证明函数f(x)不是奇函数;
(2)判断函数f(x)的单调性,并利用函数单调性的定义给出证明;
(3)若f(x)是奇函数,且f(x)﹣x2+4x≥m在x∈[﹣2,2]时恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)(万元)满足R(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)要使甲厂有盈利,求产量x的范围;
(3)甲厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数y=f(x),如果存在区间[m,n]D,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].
则称[m,n]是该函数的“和谐区间”.
(1)证明:[0,1]是函数y=f(x)=x2的一个“和谐区间”.
(2)求证:函数 ![]() 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数 ![]() (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(II)设函数![]() 存在两个极值点,并记作
存在两个极值点,并记作![]() ,若
,若![]() ,求正数
,求正数![]() 的取值范围;
的取值范围;
(III)求证:当![]() =1时,
=1时, ![]() (其中e为自然对数的底数)
(其中e为自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com