
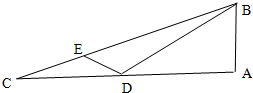
 如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.
如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$. 分析 经E点作EF⊥AC于F点,设AB=x,则由题意可求得BD,AD,AC,BC2,EF,ED,△EDB中,由余弦定理,整理可得:5x2-8$\sqrt{3}$x-12=0,可解得x,从而可求BC.
解答 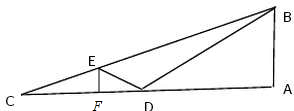
解:如图,经E点作EF⊥AC于F点,设AB=x,则由题意可得,
BD=2x,AD=$\sqrt{3}$x,AC=3+$\sqrt{3}$x,BC2=x2+(3+$\sqrt{3}$x)2,
∵△CEF∽△ABC,∴$\frac{EF}{AB}=\frac{EC}{BC}$=$\frac{1}{5}$,即有EF=$\frac{1}{5}$x,
∵∠BDE=120°,AB=$\frac{1}{2}$BD,
∴∠EDF=30°,∴ED=2EF=$\frac{2}{5}$x,
∴△EDB中,由余弦定理知:BE2=DE2+BD2-2ED×BD×cos120°
=$\frac{4}{25}$x2+4x2-2×$\frac{2}{5}$x×2x×(-$\frac{1}{2}$)=$\frac{16}{25}$BC2
=$\frac{16}{25}$[x2+(3+$\sqrt{3}$x)2],
整理可得:5x2-8$\sqrt{3}$x-12=0,
∴可解得:x=2$\sqrt{3}$或-$\frac{2\sqrt{3}}{5}$(舍去),
∴BC2=x2+(3+$\sqrt{3}$x)2=93,可解得:BC=$\sqrt{93}$.
故答案为:$\sqrt{93}$.
点评 本题主要考察了余弦定理的应用,属于中档题.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,1+$\sqrt{3}$] | B. | [0,1+$\sqrt{3}$] | C. | [-1-$\sqrt{3}$,1+$\sqrt{3}$] | D. | [-1-$\sqrt{3}$,0)∪(0,1+$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$]k∈Z | B. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$]k∈Z | ||
| C. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$]k∈Z | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$]k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0]∪[$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0)∪[$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-∞,-2)∪(-1,+∞) | C. | $(-\root{3}{{\frac{3}{2}}},-1)$ | D. | $(-∞,-\root{3}{{\frac{3}{2}}})∪(-1,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com