
已知圆 ,直线
,直线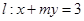 .
.
(Ⅰ)若 与
与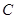 相切,求
相切,求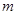 的值;
的值;
(Ⅱ)是否存在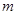 值,使得
值,使得 与
与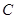 相交于
相交于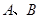 两点,且
两点,且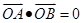 (其中
(其中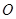 为坐标原点),若存在,求出
为坐标原点),若存在,求出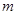 ,若不存在,请说明理由.
,若不存在,请说明理由.
(Ⅰ) (Ⅱ)m=9±2
(Ⅱ)m=9±2
解析试题分析:(Ⅰ)由圆方程配方得(x+1)2+(y-3)2=9,
圆心为C(-1,3),半径为 r = 3, 2分
若 l与C相切,则得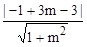 =3,
=3,
∴(3m-4)2=9(1+m2),∴m = . 5分
. 5分
(Ⅱ)假设存在m满足题意。
由 ,消去x得
,消去x得
(m2+1)y2-(8m+6)y+16=0,
由△=(8m+6)2-4(m2+1)·16>0,得m> , 8分
, 8分
设A(x1,y1),B(x2,y2),则y1+y2=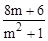 ,y1y2=
,y1y2=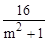 .
.
 OA·OB=x1x2+y1y2
OA·OB=x1x2+y1y2
=(3-my1)(3-my2)+y1y2
=9-3m(y1+y2)+(m2+1)y1y2
=9-3m·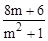 +(m2+1)·
+(m2+1)·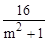
=25-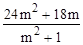 =0 10分
=0 10分
24m2+18m=25m2+25,m2-18m+25=0,
∴m=9±2 ,适合m>
,适合m> ,
,
∴存在m=9±2 符合要求.
符合要求.
考点:直线与圆相切相交的位置关系
点评:直线与圆相切,一般用圆心到直线的距离等于圆的半径,本题直线与圆相交联立方程利用韦达定理可得到焦点坐标与方程的关系,进而可将向量坐标化化简


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,点
中,点 ,直线
,直线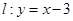 。设圆
。设圆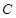 的半径为
的半径为 ,圆心在
,圆心在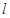 上。
上。
(1)若圆心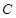 也在直线
也在直线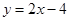 上,过点
上,过点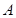 作圆
作圆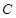 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆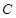 上存在点
上存在点 ,使
,使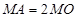 ,求圆心
,求圆心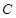 的横坐标
的横坐标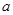 的取值范围。.
的取值范围。.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,圆O1与圆O2的半径都是1,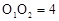 ,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得
,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得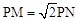 试建立适当的坐标系,并求动点P的轨迹方程
试建立适当的坐标系,并求动点P的轨迹方程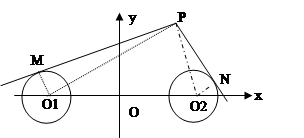
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
已知圆M过两点C(1,-1)、D(-1,1)且圆心M在直线x+y-2=0上。
(1)、求圆M的方程
(2)、设P是直线3x+4y+8=0上的动点,PA、PB是圆M的两条切线,A、B为切点,求四边形PAMB的面积的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com