
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.

其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图

以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
【答案】(1)0.024;(2)分布列见解析,![]() ;(3)
;(3)![]()
【解析】
(1)由题意可知,若一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16,则该套净水系统中一个一级过滤器需要更换8个滤芯,两个二级过滤器均需要更换4个滤芯,而由一级滤芯更换频数分布表和二级滤芯更换频数条形图可知,一级过滤器需要更换8个滤芯的概率为0.6,二级过滤器需要更换4个滤芯的概率为0.2,再由乘法原理可求出概率;
(2)由二级滤芯更换频数条形图可知,一个二级过滤器需要更换滤芯的个数为4,5,6的概率分别为0.2,0.4,0.4,而![]() 的可能取值为8,9,10,11,12,然后求出概率,可得到
的可能取值为8,9,10,11,12,然后求出概率,可得到![]() 的分布列及数学期望;
的分布列及数学期望;
(3)由![]() ,且
,且![]() ,可知若
,可知若![]() ,则
,则![]() ,或若
,或若![]() ,则
,则![]() ,再分别计算两种情况下的所需总费用的期望值比较大小即可.
,再分别计算两种情况下的所需总费用的期望值比较大小即可.
(1)由题意知,若一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16,则该套净水系统中一个一级过滤器需要更换8个滤芯,两个二级过滤器均需要更换4个滤芯,设“一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16”为事件![]() ,
,
因为一个一级过滤器需要更换8个滤芯的概率为0.6,二级过滤器需要更换4个滤芯的概率为0.2,所以![]() .
.
(2)由柱状图知,一个二级过滤器需要更换滤芯的个数为4,5,6的概率分别为0.2,0.4,0.4,由题意![]() 的可能取值为8,9,10,11,12,
的可能取值为8,9,10,11,12,
从而![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列为
的分布列为
| 8 | 9 | 10 | 11 | 12 |
| 0.04 | 0.16 | 0.32 | 0.32 | 0.16 |
![]() (个).
(个).
或用分数表示也可以为
| 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
![]() (个).
(个).
(3)解法一:记![]() 表示该客户的净水系统在使用期内购买各级滤芯所需总费用(单位:元)
表示该客户的净水系统在使用期内购买各级滤芯所需总费用(单位:元)
因为![]() ,且
,且![]() ,
,
1°若![]() ,则
,则![]() ,
,
![]() (元);
(元);
2°若![]() ,则
,则![]() ,
,
![]() (元).
(元).
因为![]() ,故选择方案:
,故选择方案:![]() .
.
解法二:记![]() 分别表示该客户的净水系统在使用期内购买一级滤芯和二级滤芯所需费用(单位:元)
分别表示该客户的净水系统在使用期内购买一级滤芯和二级滤芯所需费用(单位:元)
1°若![]() ,则
,则![]() ,
,
![]() 的分布列为
的分布列为
| 1280 | 1680 |
| 0.6 | 0.4 |
| 880 | 1080 |
| 0.84 | 0.16 |
该客户的净水系统在使用期内购买的各级滤芯所需总费用为![]() (元);
(元);
2°若![]() ,则
,则![]() ,
,
![]() 的分布列为
的分布列为
| 800 | 1000 | 1200 |
| 0.52 | 0.32 | 0.16 |
![]() (元).
(元).
因为![]()
所以选择方案:![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 两焦点分别为
两焦点分别为![]() 是椭圆在第一象限弧上一点,并满足
是椭圆在第一象限弧上一点,并满足![]() ,过P作倾斜角互补的两条直线
,过P作倾斜角互补的两条直线![]() 分别交椭圆于
分别交椭圆于![]() 两点.
两点.
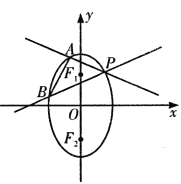
(1)求![]() 点坐标;
点坐标;
(2)求证:直线![]() 的斜率为定值;
的斜率为定值;
(3)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠BAC≠60°,过点B、C分别作△ABC外接圆的切线BD、CE,且满足![]() ,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:
,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月8日,中共中央国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当![]() 时,y是x的二次函数;当
时,y是x的二次函数;当![]() 时,
时,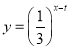 测得数据如下表(部分):
测得数据如下表(部分):
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式![]() ;
;
(2)当该产品中的新材料含量x为何值时,产品的性能指标值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P—ABCD中,PA⊥平面ABCD,∠DAB=∠ADC=90°,DC=![]() AB,F,M分别是线段PC,PB的中点.
AB,F,M分别是线段PC,PB的中点.

(1)在线段AB上找出一点N,使得平面CMN∥平面PAD,并给出证明过程;
(2)若PA=![]() AB,DC=
AB,DC=![]() AD,求二面角C—AF—D的余弦值.
AD,求二面角C—AF—D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (e为自然对数的底数,e=2.71828……),函数
(e为自然对数的底数,e=2.71828……),函数![]() 图象关于直线
图象关于直线![]() 对称,函数
对称,函数![]() 的最小值为m.
的最小值为m.
(I)求曲线![]() 的切线方程;
的切线方程;
(Ⅱ)求证:![]() ;
;
(III)求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山东省于2015年设立了水下考古研究中心,以此推动全省的水下考古、水下文化遗产保护等工作;水下考古研究中心工作站,分别设在位于刘公岛的中国甲午战争博物院和威海市博物馆。为对刘公岛周边海域水底情况进行详细了解,然后再选择合适的时机下水探摸、打捞,省水下考古中心在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业,其用氧量包含以下三个方面:
米到水底进行考古作业,其用氧量包含以下三个方面:
①下潜平均速度为![]() 米/分钟,每分钟的用氧量为
米/分钟,每分钟的用氧量为![]() 升;
升;
②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.4升;
③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为0.32升.
米/分钟,每分钟用氧量为0.32升.
潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(Ⅰ)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)若![]() ,水底作业时间为20分钟,求总用氧量
,水底作业时间为20分钟,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,已知点A(1,0)和点B(﹣1,0),![]() ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点.

(1)若x=![]() ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求![]() 的最小值;
的最小值;
(2)若![]() R,求
R,求![]() 的最大值及对应的x值.
的最大值及对应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,
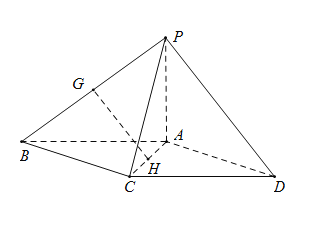
(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com