
【题目】已知函数![]() .
.
(1)证明:![]() 在区间
在区间![]() 上存在唯一零点;
上存在唯一零点;
(2)令![]() ,若
,若![]() 时
时![]() 有最大值,求实数
有最大值,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)对![]() 求导得到
求导得到![]() ,再对
,再对![]() 求导,得到
求导,得到![]() ,根据
,根据![]() 的正负,得到
的正负,得到![]() 的单调性,再由定义域求出
的单调性,再由定义域求出![]() 的正负,从而得到
的正负,从而得到![]() 的单调性,由零点存在定理,进行证明;(2)对
的单调性,由零点存在定理,进行证明;(2)对![]() 求导,得到
求导,得到![]() ,令
,令![]() ,根据(1)的结论,可得
,根据(1)的结论,可得![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,再按
,再按![]() 和
和![]() 进行分类,分别研究
进行分类,分别研究![]() 的单调性,从而得到
的单调性,从而得到![]() 有最大值时对
有最大值时对![]() 的要求,得到答案.
的要求,得到答案.
(1)![]()
易知![]() 在区间
在区间![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 单调递减
单调递减
所以![]() =0,即f(x)在
=0,即f(x)在![]() 单调递增,
单调递增,
又![]() ,则
,则![]() 在区间
在区间![]() 必存在唯一零点
必存在唯一零点
(2)![]()
所以![]()
令![]() ,则
,则![]()
由(1)知:则![]() 在
在![]() 单调递增
单调递增
又![]() ,即
,即![]() 在
在![]() 上有唯一零点
上有唯一零点![]()
当![]() 时,由
时,由![]() 得
得![]() ,所以
,所以![]() 在区间
在区间![]() 单调递增;在区间
单调递增;在区间![]() 单调递减;此时h(x)存在最大值h(0),满足题意;
单调递减;此时h(x)存在最大值h(0),满足题意;
当![]() 时,由
时,由![]() 有两个不同零点x=0及
有两个不同零点x=0及![]() ,所以h(x)在区间(0,a)单调递减;在区间
,所以h(x)在区间(0,a)单调递减;在区间![]() ,
,![]() 单调递增;此时h(x)有极大值h(0)=2a
单调递增;此时h(x)有极大值h(0)=2a
由h(x)有最大值,可得;![]() ,解得
,解得![]() ,即
,即![]()
综上所述:当![]() 时,h(x)在
时,h(x)在![]() 有最大值
有最大值


科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从使用A和B两款订餐软件的商家中分别随机抽取50个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如图.
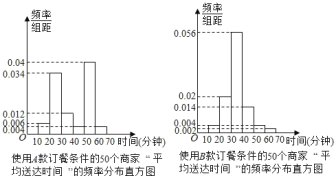
(1)试估计使用A款订餐软件的50个商家的“平均送达时间”的众数及平均数;
(2)根据以上抽样调查数据,回答以下问题:
(ⅰ)为了解如何降低各商家的送餐时间,我们先从这100家商家里选出平均送达时间不超过20分钟的商家,然后再从中随机挑选两家进行跟踪研究,求恰好所抽中的商家均为使用B款软件的概率.
(ⅱ)如果你要从A和B两款订餐软件中选择一款订餐,你会选择哪款?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为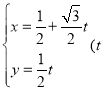 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓减人口老年化带来的问题,中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策,生“二孩”是目前中国比较流行的元素![]() 某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”
某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”![]() 现已得知100人中同意父母生“二孩”占
现已得知100人中同意父母生“二孩”占![]() ,统计情况如表:
,统计情况如表:
性别属性 | 同意父母生“二孩” | 反对父母生“二孩” | 合计 |
男生 | 10 | ||
女生 | 30 | ||
合计 | 100 |
![]() 请补充完整上述列联表;
请补充完整上述列联表;
![]() 根据以上资料你是否有
根据以上资料你是否有![]() 把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
参考公式与数据:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相同数字的概率;
(Ⅱ)求取出的两个球上标号之积能被3整除的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +
+![]() .
.
(1)当m=0时,求不等式f(x)≤9的解集;
(2)当m=2时,若x∈(1,4),f(x) ![]() 2x
2x![]() a<0,求a的取值范围.
a<0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后, 某科技企业为抓住“一带一路”带来的机遇, 决定开发生产一款大型电子设备, 生产这种设备的年固定成本为![]() 万元, 每生产
万元, 每生产![]() 台,需另投入成本
台,需另投入成本![]() (万元), 当年产量不足
(万元), 当年产量不足![]() 台时,
台时,![]() (万元); 当年产量不小于
(万元); 当年产量不小于![]() 台时
台时![]() (万元), 若每台设备售价为
(万元), 若每台设备售价为![]() 万元, 通过市场分析,该企业生产的电子设备能全部售完.
万元, 通过市场分析,该企业生产的电子设备能全部售完.
(1)求年利润![]() (万元)关于年产量
(万元)关于年产量![]() (台)的函数关系式;
(台)的函数关系式;
(2)年产量为多少台时 ,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com