
【题目】设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2 , 且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞)
【答案】B
【解析】解:∵f(﹣x)+f(x)=x2 , ∴f(x)﹣ ![]() x2 +f(﹣x)﹣
x2 +f(﹣x)﹣ ![]() x2 =0,
x2 =0,
令g(x)=f(x)﹣ ![]() x2 , ∵g(﹣x)+g(x)=f(﹣x)﹣
x2 , ∵g(﹣x)+g(x)=f(﹣x)﹣ ![]() x2+f(x)﹣
x2+f(x)﹣ ![]() x2=0,
x2=0,
∴函数g(x)为奇函数.
∵x∈(0,+∞)时,f′(x)>x.
∴x∈(0,+∞)时,g′(x)=f′(x)﹣x>0,故函数g(x)在(0,+∞)上是增函数,
故函数g(x)在(﹣∞,0)上也是增函数,由f(0)=0,可得g(x)在R上是增函数.
f(2﹣a)﹣f(a)≥2﹣2a,等价于f(2﹣a)﹣ ![]() ≥f(a)﹣
≥f(a)﹣ ![]() ,
,
即g(2﹣a)≥g(a),∴2﹣a≥a,解得a≤1,
故选:B.
【考点精析】关于本题考查的基本求导法则,需要了解若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣lnx(a∈R)
(1)当a=1时,求函数y=f(x)的单调区间;
(2)若x∈(0,1],|f(x)|≥1恒成立,求a的取值范围;
(3)若a= ![]() ,证明:ex﹣1f(x)≥x.
,证明:ex﹣1f(x)≥x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学准备在开学时举行一次大学一年级学生座谈会,拟邀请20名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
学院 | 机械工程学院 | 海洋学院 | 医学院 | 经济学院 |
人数 | 4 | 6 | 4 | 6 |
(Ⅰ)从这20名学生中随机选出3名学生发言,求这3名学生中任意两个均不属于同一学院的概率;
(Ⅱ)从这20名学生中随机选出3名学生发言,设来自医学院的学生数为ξ,求随机变量ξ的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的短轴长为2,离心率e=
=1(a>b>0)的短轴长为2,离心率e= ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+m与椭圆交于不同的两点A,B,与圆x2+y2= ![]() 相切于点M.
相切于点M.
(i)证明:OA⊥OB(O为坐标原点);
(ii)设λ= ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 
(1)求证AM∥平面BDE;
(2)求二面角A﹣DF﹣B的大小;
(3)试在线段AC上一点P,使得PF与CD所成的角是60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2 , 且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设0<a<1,已知函数f(x)= 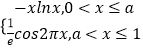 ,若对任意b∈(0,
,若对任意b∈(0, ![]() ),函数g(x)=f(x)﹣b至少有两个零点,则a的取值范围是( )
),函数g(x)=f(x)﹣b至少有两个零点,则a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)= ![]() +|lnx﹣a|,x∈[1,e2].
+|lnx﹣a|,x∈[1,e2].
(1)当a=3时,求曲线y=f(x)在点(3,f(3))处的切线方程;
(2)若f(x)≤ ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com