
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:

(1)根据列联表,能否有99.9%的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从40岁以下的被调查者中用分层抽样的方式抽取了5名,现从这5名被调查者中随机选取3名,求这3名被调查者中恰有1名对手机游戏无兴趣的概率.
附: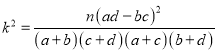
参考数据:

科目:高中数学 来源: 题型:
【题目】设数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将两个数列的偏差距离定义为
,则将两个数列的偏差距离定义为![]() ,其中
,其中![]() .
.
(1)求数列1,2,7,8和数列2,3,5,6的偏差距离;
(2)设![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,
的集合,![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() ,若
,若![]() ,
,![]() ,
,![]() 和
和![]() 的偏差距离小于2020,求
的偏差距离小于2020,求![]() 最大值;
最大值;
(3)记![]() 是所有7项数列
是所有7项数列![]() 或
或![]() 的集合,
的集合,![]() ,且
,且![]() 中任何两个元素的偏差距离大于或等于3,证明:
中任何两个元素的偏差距离大于或等于3,证明:![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,对坐标平面上任意一点
,对坐标平面上任意一点![]() ,定义
,定义![]() ,若两点
,若两点![]() ,
,![]() ,满足
,满足![]() ,称点
,称点![]() ,
,![]() 在曲线
在曲线![]() 同侧;
同侧;![]() ,称点
,称点![]() ,
,![]() 在曲线
在曲线![]() 两侧.
两侧.
(1)直线![]() 过原点,线段
过原点,线段![]() 上所有点都在直线
上所有点都在直线![]() 同侧,其中
同侧,其中![]() ,
,![]() ,求直线
,求直线![]() 的倾斜角的取值范围;
的倾斜角的取值范围;
(2)已知曲线![]() ,
,![]() 为坐标原点,求点集
为坐标原点,求点集![]() 的面积;
的面积;
(3)记到点![]() 与到
与到![]() 轴距离和为
轴距离和为![]() 的点的轨迹为曲线
的点的轨迹为曲线![]() ,曲线
,曲线![]() ,若曲线
,若曲线![]() 上总存在两点
上总存在两点![]() ,
,![]() 在曲线
在曲线![]() 两侧,求曲线
两侧,求曲线![]() 的方程与实数
的方程与实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减,②存在常数
上单调递减,②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“渐近函数”.
的“渐近函数”.
(1)判断函数![]() 是不是函数
是不是函数![]() 的“渐近函数”,说明理由;
的“渐近函数”,说明理由;
(2)求证:函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(3)若函数![]() ,
,![]() ,求证:当且仅当
,求证:当且仅当![]() 时,
时,![]() 是
是![]() 的“渐近函数”.
的“渐近函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 各项不为0,前
各项不为0,前![]() 项和为
项和为![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)在(1)的条件下,已知![]() ,分别求
,分别求![]() 和
和![]() 的表达式;
的表达式;
(3)证明:![]() 是等差数列的充要条件是:对任意
是等差数列的充要条件是:对任意![]() ,都有:
,都有:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,动点P与定点![]() 的距离和它到定直线
的距离和它到定直线![]() 的距离之比是
的距离之比是![]() ,设动点P的轨迹为E.
,设动点P的轨迹为E.
(1)求动点P的轨迹E的方程;
(2)设过F的直线交轨迹E的弦为AB,过原点的直线交轨迹E的弦为CD,若![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com