
【题目】已知抛物线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,以
时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)与![]() 平行的直线
平行的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,若平行线
两点,若平行线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,且
,且![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求
倍,求![]() 和
和![]() 的方程.
的方程.
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若某校研究性学习小组共6人,计划同时参观科普展,该科普展共有甲,乙,丙三个展厅,6人各自随机地确定参观顺序,在每个展厅参观一小时后去其他展厅,所有展厅参观结束后集合返回,设事件A为:在参观的第一小时时间内,甲,乙,丙三个展厅恰好分别有该小组的2个人;事件B为:在参观的第二个小时时间内,该小组在甲展厅人数恰好为2人,则![]() ( ).
( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型综艺节目,《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的![]() 根据调查显示,是否喜欢盲拧魔方与性别有关
根据调查显示,是否喜欢盲拧魔方与性别有关![]() 为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如表
为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如表![]() 所示,并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如表
所示,并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如表![]() 所示.
所示.


(Ⅰ)将表![]() 补充完整,并判断能否在犯错误的概率不超过
补充完整,并判断能否在犯错误的概率不超过![]() 的前提下认为是否喜欢盲拧与性别有关?
的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表![]() 中成功完成时间在
中成功完成时间在![]() 和
和![]() 这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
附参考公式及数据: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
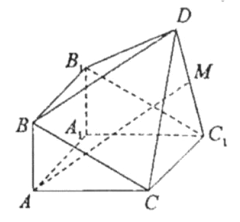
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+2xtanθ-1,x∈[-1,![]() ],其中θ∈(-
],其中θ∈(-![]() ,
,![]() ).
).
(1)当θ=-![]() 时,求函数f(x)的最大值;
时,求函数f(x)的最大值;
(2)求θ的取值范围,使y=f(x)在区间[-1,![]() ]上是单调函数.
]上是单调函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com