
【题目】给出以下命题:
(1)已知回归直线方程为![]() ,样本点的中心为
,样本点的中心为![]() ,则
,则![]() ;
;
(2)已知![]() ,
,![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() 是
是![]() 的充要条件;
的充要条件;
(3)函数![]() 图象关于点
图象关于点![]() 对称且在
对称且在![]() 上单调递增;
上单调递增;
(4)命题“存在![]() ”的否定是“对于任意
”的否定是“对于任意![]() ”;
”;
(5)设函数![]() ,若函数
,若函数![]() 恰有三个零点,则实数m的取值范围为
恰有三个零点,则实数m的取值范围为![]() .
.
其中不正确的命题序号为______________ .
【答案】(2)(4)(5)
【解析】
根据线性回归直线的性质、充分必要条件的定义、正弦型函数的性质、命题的否定、函数的零点等知识对各个命题进行判断.
(1)根据回归直线恒过样本的中心点,可得![]() ,故正确;
,故正确;
(2)由![]() 有
有![]() ,
,![]() 与
与![]() 的夹角为钝角或平角,所以根据充要条件的定义可判断错误.故错误;
的夹角为钝角或平角,所以根据充要条件的定义可判断错误.故错误;
(3)把![]() 代入函数
代入函数![]() ,函数值为
,函数值为![]() ,所以函数
,所以函数![]() 关于
关于![]() 对称,由
对称,由![]() ,可得
,可得![]() 所以函数在
所以函数在![]() 上是递增的.所以函数在
上是递增的.所以函数在![]() 上是递增的.故正确;
上是递增的.故正确;
(4)命题“存在![]() ,
,![]() ”的否定是“对于任意
”的否定是“对于任意![]() ,
,![]() ”故错误;
”故错误;
(5)构造函数![]() ,要使函数
,要使函数![]() 恰有三个零点,必须使函数
恰有三个零点,必须使函数![]() 有零点,并且函数
有零点,并且函数![]() 有两个零点,而函数
有两个零点,而函数![]() 在
在![]() 上的两个零点为-1和-2,从而得到
上的两个零点为-1和-2,从而得到![]() ,故是错误的.
,故是错误的.
故答案为:(2)(4)(5).


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是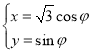 (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,等边
,等边![]() 的顶点都在
的顶点都在![]() 上,且点
上,且点![]() ,
,![]() ,
,![]() 按照逆时针方向排列,点
按照逆时针方向排列,点![]() 的极坐标为
的极坐标为![]() .
.
(Ⅰ)求点![]() ,
,![]() ,
,![]() 的直角坐标;
的直角坐标;
(Ⅱ)设![]() 为
为![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①存在实数![]() ,
,![]() ,使得
,使得![]() ;
;
②“![]() ,
,![]() ”的否定是“存在
”的否定是“存在![]() ,
,![]() ”;
”;
③掷一枚质地均匀的正方体骰子,向上的点数不小于3的概率为![]() ;
;
④在闭区间![]() 上取一个随机数
上取一个随机数![]() ,则
,则![]() 的概率为
的概率为![]() .
.
其中所有的真命题为________.(填写所有正确的结论序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() 中底面边长、侧棱长都是4,
中底面边长、侧棱长都是4,![]() 别是
别是![]() 的中点,则以下四个结论中正确的是( )
的中点,则以下四个结论中正确的是( )
①![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;②
;②![]() 平行于平面
平行于平面![]() ;③三棱锥
;③三棱锥![]() 的体积为
的体积为![]() ;④
;④![]() 垂直于
垂直于![]() .
.
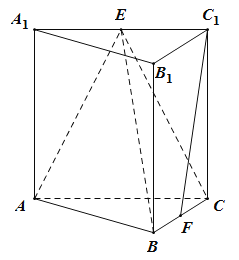
A.①②③B.②③④C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 与
与![]() 的离心率相等.椭圆
的离心率相等.椭圆![]() 的右焦点为F,过点F的直线与椭圆
的右焦点为F,过点F的直线与椭圆![]() 交于A,B两点,射线
交于A,B两点,射线![]() 与椭圆
与椭圆![]() 交于点C,椭圆
交于点C,椭圆![]() 的右顶点为D.
的右顶点为D.
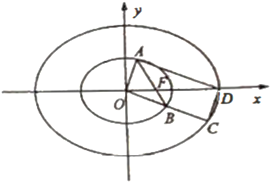
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若![]() ,求证:四边形
,求证:四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示校情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续![]() 天每天新增感染人数不超过
天每天新增感染人数不超过![]() 人”,根据连续
人”,根据连续![]() 天的新增病例数计算,下列各项选项中,一定符合上述指标的是( )
天的新增病例数计算,下列各项选项中,一定符合上述指标的是( )
①平均数![]() ;
;
②标准差![]() ;
;
③平均数![]() ;且标准差
;且标准差![]() ;
;
④平均数![]() ;且极差小于或等于
;且极差小于或等于![]() ;
;
⑤众数等于![]() 且极差小于或等于
且极差小于或等于![]() .
.
A.①②B.③④C.③④⑤D.④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种产品的质量,从中分别随机抽取了10件样品,测量产品中某种元素的含量(单位:毫克),如图所示是测量数据的茎叶图.规定:当产品中的此中元素的含量不小于18毫克时,该产品为优等品.
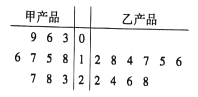
(1)试用样品数据估计甲、乙两种产品的优等品率;
(2)从乙产品抽取的10件样品中随机抽取3件,求抽到的3件样品中优等品数![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(3)从甲产品抽取的10件样品中有放回地随机抽取3件,也从乙产品抽取的10件样品中有放回地随机抽取3件;抽到的优等品中,记“甲产品恰比乙产品多2件”为事件![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
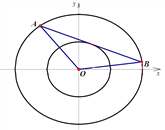
【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”.已知椭圆![]() ,以椭圆
,以椭圆![]() 的焦点为顶点作相似椭圆
的焦点为顶点作相似椭圆![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与椭圆
两点,且与椭圆![]() 仅有一个公共点,试判断
仅有一个公共点,试判断![]() 的面积是否为定值(
的面积是否为定值(![]() 为坐标原点)?若是,求出该定值;若不是,请说明理由.
为坐标原点)?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一条线段,且
上的一条线段,且![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的动点,则
上的动点,则
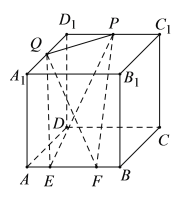
①四面体![]() 的体积为定值
的体积为定值
②直线![]() 到平面
到平面![]() 的距离为定值
的距离为定值
③点![]() 到直线
到直线![]() 的距离为定值
的距离为定值
④直线![]() 与平面
与平面![]() 所成的角为定值
所成的角为定值
其中正确结论的编号是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com