
【题目】某企业生产的一种产品的广告费用![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)的统计数据如下表:
(单位:万元)的统计数据如下表:
广告费用 |
|
|
|
|
|
销售额 |
|
|
|
|
|
(1)根据上述数据,求出销售额![]() (万元)关于广告费用
(万元)关于广告费用![]() (万元)的线性回归方程;
(万元)的线性回归方程;
(2)如果企业要求该产品的销售额不少于![]() 万元,则投入的广告费用应不少于多少万元?
万元,则投入的广告费用应不少于多少万元?
(参考数值: ![]() .
.
回归直线的斜率和截距的最小二乘法估计公式分别为: 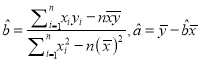 )
)
【答案】(1)![]() (2)投入的广告费用应不少于
(2)投入的广告费用应不少于![]() 万元
万元
【解析】试题分析:(1)由公式 求得
求得![]() 的值,再根据表格数据先求出样本的中心点坐标,代入回归方程可求得
的值,再根据表格数据先求出样本的中心点坐标,代入回归方程可求得![]() 的值即可确定线性回归方程;(2)根据回归方程,由
的值即可确定线性回归方程;(2)根据回归方程,由![]() 可得结果.
可得结果.
试题解析:(1)由表格数据可得 ![]() ,
,  ,
, ![]() ,
, ![]() 所求回归直线方程为
所求回归直线方程为![]() .
.
(2)![]() (万元).
(万元).
答:投入的广告费用应不少于![]() 万元.
万元.
【方法点晴】本题主要考查线性回归方程及其应用,属于中档题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某软件公司新开发一款学习软件,该软件把学科知识设计为由易到难共12关的闯关游戏.为了激发闯关热情,每闯过一关都奖励若干慧币(一种网络虚拟币).该软件提供了三种奖励方案:第一种,每闯过一关奖励40慧币;第二种,闯过第一关奖励40慧币,以后每一关比前一关多奖励4慧币;第三种,闯过第一关奖励慧币,以后每一关比前一关奖励翻一番(即增加1倍).游戏规定:闯关者须于闯关前任选一种奖励方案.
(1)设闯过![]() 关后三种奖励方案获得的慧币总数依次为
关后三种奖励方案获得的慧币总数依次为![]() ,试求出
,试求出![]() 的表达式;
的表达式;
(2)如果你是一名闯关者,为了得到更多的慧币,你应如何选择奖励方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为
米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为![]() 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为![]() 升;②水底作业时间范围是最少
升;②水底作业时间范围是最少![]() 分钟最多
分钟最多![]() 分钟,每分钟用氧量为
分钟,每分钟用氧量为![]() 升;③返回水面时,平均速度为
升;③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为![]() 升.潜水员在此次考古活动中的总用氧量为
升.潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(1)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,水底作业时间为
,水底作业时间为![]() 分钟,求总用氧量
分钟,求总用氧量![]() 的取值范围;
的取值范围;
(3)若潜水员携带氧气![]() 升,请问潜水员最多在水下多少分钟(结果取整数)?
升,请问潜水员最多在水下多少分钟(结果取整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位同学家里订了一份报纸,送报人每天都在早上6 : 207 : 40之间将报纸送达,该同学需要早上7 : 008 : 00之间出发上学,则这位同学在离开家之前能拿到报纸的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科)(本小题满分12分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号 | 分组 | 频数 | 频率 |
第一组 | [230,235) | 8 | 0.16 |
第二组 | [235,240) | ① | 0.24 |
第三组 | [240,245) | 15 | ② |
第四组 | [245,250) | 10 | 0.20 |
第五组 | [250,255] | 5 | 0.10 |
合 计 | 50 | 1.00 | |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示,下面结论正确的个数是( )
的部分图象如图所示,下面结论正确的个数是( )
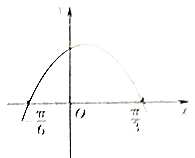
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
③函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④函数![]() 的图象可由函数
的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到
个单位长度得到
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com