
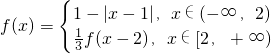 ,则函数F(x)=xf(x)-1零点个数为
,则函数F(x)=xf(x)-1零点个数为 的图象的交点个数,在同一坐标系中画出两个函数图象,数形结合可得两个函数的图象的交点个数.
的图象的交点个数,在同一坐标系中画出两个函数图象,数形结合可得两个函数的图象的交点个数.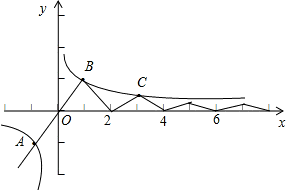 解:∵函数
解:∵函数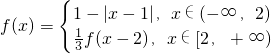 ,故函数F(x)=xf(x)-1零点个数,
,故函数F(x)=xf(x)-1零点个数, 的根的根数,即函数f(x)的图象与函数y=
的根的根数,即函数f(x)的图象与函数y= 的图象的交点个数.
的图象的交点个数. 图象共有3个交点,分别为A(-1,-1)、B(1,1)、C(3,
图象共有3个交点,分别为A(-1,-1)、B(1,1)、C(3, ),
),

科目:高中数学 来源: 题型:
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年河北省高二第二学期期末考试数学(理)试卷 题型:填空题
给出下列三个命题:
①若函数 ,则函数f(x)的极值点个数为1个。
,则函数f(x)的极值点个数为1个。
②若
 。
。
③若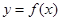 是定义在R上的函数,则
是定义在R上的函数,则 是函数
是函数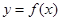 在
在 处取得极值的必要不充分条件。
处取得极值的必要不充分条件。
其中真命题是_________(把正确命题的序号都填上)。
查看答案和解析>>
科目:高中数学 来源:徐州模拟 题型:解答题
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com