
【题目】根据历年市场行情,某种农产品在4月份的30天内每吨的售价p(万元)与时间t(天)![]() 的关系如图的折线表示.又知该农产品在30天内的日交易量Q(吨)与时间t(天)满足一次函数关系,部分数据如表所示.
的关系如图的折线表示.又知该农产品在30天内的日交易量Q(吨)与时间t(天)满足一次函数关系,部分数据如表所示.

第t天 | 4 | 10 | 16 | 22 |
Q(吨) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,求出该种农产品每吨的售价p(万元)与时间t(天)所满足的函数关系式;
(2)若该农产品日交易额![]() 每吨的售价
每吨的售价![]() 日交易量,求在这30天中,该农产品日交易额y(万元)的最大值.
日交易量,求在这30天中,该农产品日交易额y(万元)的最大值.
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过短轴的一个端点与两个焦点的圆的面积为
的焦距为2,过短轴的一个端点与两个焦点的圆的面积为![]() ,过椭圆
,过椭圆![]() 的右焦点作斜率为
的右焦点作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 垂直于
垂直于![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是 _________ .

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
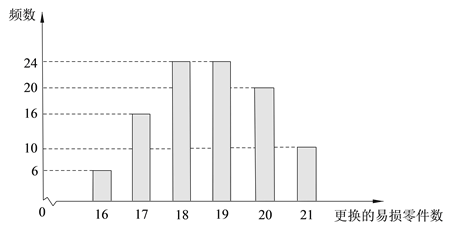
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元), ![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(Ⅰ)若![]() =19,求y与x的函数解析式;
=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于![]() ”的频率不小于0.5,求
”的频率不小于0.5,求![]() 的最小值;
的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点作垂直于椭圆长轴的直线交椭圆于
,过右焦点作垂直于椭圆长轴的直线交椭圆于![]() 两点,且
两点,且![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2) 设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() .
.
①求![]() 的值;
的值;
②求![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是一个类似计步数据库的公众账号.用户只需以运动手环或手机协处理器的运动数据为介,然后关注该公众号,就能看见自己与好友每日行走的步数,并在同一排行榜上得以体现.现随机选取朋友圈中的50人,记录了他们某一天的走路步数,并将数据整理如下:
步数/步 |
|
|
|
| 10000以上 |
男生人数/人 | 1 | 2 | 7 | 15 | 5 |
女性人数/人 | 0 | 3 | 7 | 9 | 1 |
规定:人一天行走的步数超过8000步时被系统评定为“积极性”,否则为“懈怠性”.
(1)以这50人这一天行走的步数的频率代替1人一天行走的步数发生的概率,记![]() 表示随机抽取3人中被系统评为“积极性”的人数,求
表示随机抽取3人中被系统评为“积极性”的人数,求![]() 和
和![]() 的数学期望.
的数学期望.
(2)为调查评定系统的合理性,拟从这50人中先抽取10人(男性6人,女性4人).其中男性中被系统评定为“积极性”的有4人,“懈怠性”的有2人,从中任意选取3人,记选到“积极性”的人数为![]() ;
;
其中女性中被系统评定为“积极性”和“懈怠性”的各有2人,从中任意选取2人,记选到“积极性”的人数为![]() ;求
;求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆E的标准方程;
(2)问:是否存在过点![]() 的直线l,使以直线l被椭圆E所截得的弦
的直线l,使以直线l被椭圆E所截得的弦![]() 为直径的圆过点
为直径的圆过点![]() ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC﹣A1B1C1中,D,E分别是AB,AC的中点,AB=2A1B1,B1E⊥平面ABC,且∠ACB=90°.
(Ⅰ)求证:B1C∥平面A1DE;
(Ⅱ)若AC=3BC=6,△AB1C为等边三角形,求四棱锥A1﹣B1C1ED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游区每年各个月份接待游客的人数近似地满足周期性规律,因而,第![]() 个月从事旅游服务工作的人数
个月从事旅游服务工作的人数![]() 可近似地用函数
可近似地用函数![]() 来刻画,其中,正整数
来刻画,其中,正整数![]() 表示月份,
表示月份,![]() 为正整数,
为正整数,![]() .
.
统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
(i)每年相同的月份,该地区从事旅游服务工作的人数基本相同;
(ii)该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人;
(iii)2月份该地区从事旅游服务工作的人数约为100人,随后逐月递增直到8月份达到最多.
(1)根据已知信息,试确定一个符合条件的![]() 的表达式.
的表达式.
(2)一般地,当该地区从事旅游服务工作的人数在400或400以上时,该地区也进入了一年中的旅游“旺季”.求一年中的哪几个月是该地区的旅游旺季?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com