
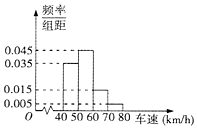
 ij�н��ܲ��Ŷ�һ·������60km/h��Ϊ����Υ��������Ծ�����·�ε�300���������м�⣬���������ݰ�[40��50����[50.60����[60��70����[70��80�������г����ij��پ���[40��80]�ڣ��ֳ����飬���Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
ij�н��ܲ��Ŷ�һ·������60km/h��Ϊ����Υ��������Ծ�����·�ε�300���������м�⣬���������ݰ�[40��50����[50.60����[60��70����[70��80�������г����ij��پ���[40��80]�ڣ��ֳ����飬���Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ��1����Ƶ�ʷֲ�ֱ��ͼ֪�����Υ�³���Ƶ��Ϊ0.8��Υ�³���Ƶ��Ϊ0.2���ɴ�����������
��2����i���ô˴μ��������ȫ�г���Υ���������ÿ����Υ�µĸ���Ϊ0.2������֪����������εĿ���ȡֵΪ0��1��2��3���ҦΡ�B��3��0.2�����ɴ��������3������Υ�³������εķֲ��м�������
��ii������֪��ÿ����Υ�µĸ���Ϊ0.2�������ٲ�����70km/h�ĸ���Ϊ0.005�����������ʼ��㹫ʽ����������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ֪����Υ�³���Ƶ��Ϊ����0.035+0.045����10=0.8��
Υ�³���Ƶ��Ϊ����0.005+0.015����10=0.2��
��˴μ�ⲻΥ�³���300��0.8=240����Υ�³���300��0.2=60����
���ֲ�����ķ������г�ȡ20������Υ�³��У�20��0.2=4����
���г��ٲ�����70km/h����20��0.005��10=1����
��2����i���ô˴μ��������ȫ�г���Υ���������ÿ����Υ�µĸ���Ϊ0.2��
����֪����������εĿ���ȡֵΪ0��1��2��3���ҦΡ�B��3��0.2����
P����=0��=0.83=0.512��
P����=1��=${C}_{3}^{1}0.2•0��{8}^{2}$=0.384��
P����=2��=${C}_{3}^{2}0��{2}^{2}•0.8=0.096$��
P����=3��=0.23=0.008��
��εķֲ���Ϊ��
| �� | 0 | 1 | 2 | 3 |
| P | 0.512 | 0.384 | 0.096 | 0.008 |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ���ֲ��������ɢ����������ķֲ�������ѧ�������������ʵ�֪ʶ������ѧ�����Ķ�����������ʶͼ�������������⡢��������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ${a_n}={10^n}-8$ | B�� | ${a_n}=\frac{{{{10}^n}-1}}{9}$ | C�� | ${a_n}={2^n}-1$ | D�� | ${a_n}=\frac{{2��{{{10}^n}-1}��}}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Ѻ���f��x��ͼ���ϸ���ĺ��������̵�ԭ����һ�루�����겻�䣩��������ƽ��$\frac{��}{4}$����λ���ȣ��ɵõ�����g��x����ͼ�� | |
| B�� | ����������ͼ�������ֱ��$x=-\frac{��}{4}$�Գ� | |
| C�� | ��������������$��-\frac{��}{4}��\frac{��}{4}��$�϶��ǵ����������� | |
| D�� | ����y=g��x����[0��2��]��ֻ��4����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2-2i | C�� | 3-i | D�� | 1+3i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��12��13�� | B�� | ��-12��13�� | C�� | ��-12��-13�� | D�� | ��12��-13�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com