
����Ŀ��Ϊ�˶�2016��ijУ�п��ɼ����з�������60�����ϵ�ȫ��ͬѧ��������8λ�����ǵ���ѧ������������Ϊ�ٷ��ƣ���С��������60��65��70��75��80��85��90��95������������С��������72��77��80��84��88��90��93��95�� �ο���ʽ�����ϵ��  ��
��
�ع�ֱ�߷����ǣ� ![]() ������
������  ��
��
�ο����ݣ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��1�����涨85������Ϊ���㣬����8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ����ĸ��ʣ�
��2������8λͬѧ����ѧ����������ѧ������ʵ�϶�Ӧ���±���
ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
��ѧ����x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
��������y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
��ѧ����z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
���ñ���y��x��z��x�����ϵ��˵����������ѧ����ѧ����ѧ����س̶ȣ�
����y��x��z��x�����Իع鷽�̣�ϵ����ȷ��0.01������ijͬѧ����ѧ�ɼ�Ϊ50��ʱ����������������ѧ���Ƶĵ÷֣�
���𰸡�
��1���⣺��8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ���㣬
����Ҫ�ȴ�����4 �����������ѡ��3������ѧ������Ӧ��
��ͬ�������� ![]() ����
���� ![]() ����
����
Ȼ��ʣ�µ�5����ѧ�������������������Ӧ����ͬ�������� ![]() ��
��
���ݳ˷�ԭ�������������IJ�ͬ������ ![]() ��
��
��8λͬѧ��������������ѧ�����ֱ��Ӧ�������� ![]() ��
��
������ĸ���Ϊ ![]()
��2���⣺�ٱ���y��x��z��x�����ϵ���ֱ���
![]() ��
��
���Կ�������������ѧ����ѧ����ѧ�ɼ����Ǹ߶�����أ�
����y��x��z��x�����Իع鷽�̷ֱ��� ![]() ��
��
�������������ݣ������
![]() ��
��
![]() ��
��
����y��x��z��x�Ļع鷽�̷ֱ���
![]() ��
�� ![]() ��
��
��x=50ʱ�� ![]() ��
��
�൱��������ѧΪ50��ʱ������������ѧ�ɼ��ֱ�ԼΪ66.85�֡�61.2��
����������1���������8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ����Ļ����¼������Լ���8λͬѧ��������������ѧ�����ֱ��Ӧ�����¼�������������ĸ���ֵ��2���ٱ���y��x��z��x�����ϵ�����ó���������ѧ����ѧ����ѧ�ɼ����Ǹ߶�����أ������y��x��z��x�����Իع鷽�̣��ɴ˼���x=50ʱy��z��ֵ���ɣ�


 ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪b��1+cosC��=c��2��cosB����
������֤��a��c��b�ɵȲ����У�
������C= ![]() ����ABC�����Ϊ4
����ABC�����Ϊ4 ![]() ����c��
����c��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڵ���Ϊֱ�����ε�����P-ABCD��,AD��BC,��ABC=90��,PA��ƽ��ABCD,PA=3,AD=2,AB=2![]() ,BC=6.
,BC=6.
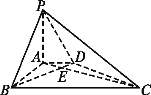
(1)��֤:BD��ƽ��PAC; (2)������P-BD-A�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ����Բ
����Բ![]() ��
��![]() �ύ��
�ύ��![]() ���㣬��
���㣬��![]() ��
��
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2�����![]() ����Բ
����Բ![]() �ϵ�һ�����㣬��ֱ��
�ϵ�һ�����㣬��ֱ��![]() ��ֱ��
��ֱ��![]() �ֱ���
�ֱ���![]() ���㣮�Ƿ���ڵ�
���㣮�Ƿ���ڵ�![]() ʹ����
ʹ����![]() Ϊֱ����Բ������
Ϊֱ����Բ������![]() �������ڣ������
�������ڣ������![]() �ĺ����ꣻ�������ڣ�˵������.
�ĺ����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
Ϊ��![]() ���е㣬
���е㣬

��1��֤����![]() ��
��
��2������![]() ��
Ϊ��![]() ��һ�㣬��
��һ�㣬��![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���н�ͨ����Ϊ�˶Ըó��й���������ǿ��ܣ����ѡȡ��100�˾ó��й���������������������ʾ����飬�����ʾ��е���100�˸��������������ֵ���ٷ��ƣ�����![]() ��
��![]() ��
��![]() ��
��![]() �ֳ�5�飬�Ƴ���ͼ��ʾƵ�ʷ�ֱ��ͼ��
�ֳ�5�飬�Ƴ���ͼ��ʾƵ�ʷ�ֱ��ͼ��

��1����ͼ��x��ֵ��
��2�����������ݵ�ƽ��������λ����
��3����֪���������ֵ��![]() �ڵ���������Ů�����ı�Ϊ
�ڵ���������Ů�����ı�Ϊ![]() ���������������ֵΪ
���������������ֵΪ![]() �����������ȡ2�˽�����̸����2�˾�Ϊ�����ĸ��ʣ�
�����������ȡ2�˽�����̸����2�˾�Ϊ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]()
![]() ����������
���������� ![]() =��2cosx��1����
=��2cosx��1���� ![]() =��cosx��
=��cosx�� ![]() sin2x����x��R��
sin2x����x��R��
��1����f��x������С�����ڣ�
��2���ڡ�ABC�У�a��b��c�ֱ��ǽ�A��B��C�ĶԱߣ�f��A��=2��a= ![]() ��b+c=3��b��c������b��c��ֵ��
��b+c=3��b��c������b��c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ������
������![]() .
.
��1����![]() ��
��![]() ����ֵ��
����ֵ��
��2����![]() ����㣬��ʵ��
����㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() �������������
�������������![]() ��
��![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A��{x|2��x��8}��B��{x|1<x<6}��C��{x|x>a}��U��R��
(1)��A��B��(CUA)��B��
(2)��A��C��![]() ����a��ȡֵ��Χ��
����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com