[题目]如图:某快递小哥从A地出发.沿小路以平均时速20公里/小时.送快件到C处.已知...是等腰三角形..(1)试问.快递小哥能否在50分钟内将快件送到C处?(2)快递小哥出发15分钟后.快递公司发现快件有重大问题.由于通讯不畅.公司只能派车沿大路追赶.若汽车平均时速60公里/小时.问.汽车能否先到达C处?参考值:.. . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图：某快递小哥从A地出发，沿小路以平均时速20公里/小时，送快件到C处，已知（公里），，，是等腰三角形，.

（1）试问，快递小哥能否在50分钟内将快件送到C处？

（2）快递小哥出发15分钟后，快递公司发现快件有重大问题，由于通讯不畅，公司只能派车沿大路追赶，若汽车平均时速60公里/小时，问，汽车能否先到达C处？

参考值：，， .

【答案】（1）不能；（2）能.

【解析】

（1）根据正弦定理求得，再利用路程除以速度得到到达C处所用的时间，即可得答案；

（2）利用余弦定理求出的值，再计算汽车到达C处所用的时间，即可得答案；

（1）在中，，由，得，

于是，由

可知，快递小哥不能在50分钟内将快件送到C处.

（2）在中，由，得，

在中，，由，得，

由

可知，汽车能先到达C处.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知四棱锥中，面面，底面为矩形，且，，，O为的中点，点E在上，且．

（1）证明：；

（2）在上是否存在一点F，使面，若存在，试确定点F的位置．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】5人并排站成一行，如果甲乙两人不相邻，那么不同的排法种数是__________.(用数字作答)；5人并排站成一行，甲乙两人之间恰好有一人的概率是__________(用数字作答)

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标系中，直线的参数方程为（为参数，为直线的倾斜角），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）写出曲线的直角坐标方程，并求时直线的普通方程；

（2）若直线和曲线交于两点，点的直角坐标为，求的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的焦点坐标为，，过垂直于长轴的直线交椭圆于、两点，且.

（1）求椭圆的方程；

（2）过的直线与椭圆交于不同的两点、，则的内切圆的面积是否存在最大值？若存在求出这个最大值及此时的直线方程；若不存在，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

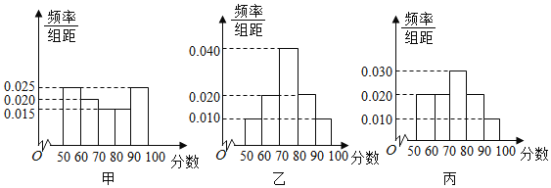
【题目】甲、乙、丙三位同学在一项集训中的40次测试分数都在[50，100]内，将他们的测试分数分别绘制成频率分布直方图，如图所示，记甲、乙、丙的分数标准差分别为s1，s2，s3，则它们的大小关系为( )

A.s1s2s3B.s1s3s2

C.s3s1s2D.s3s2s1

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】天干地支纪年法，源于中国.中国自古便有十天干与十二地支.十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸，十二地支即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配，排列起来，天干在前，地支在后，天干由“甲”起，地支由“子”起，比如说第一年为“甲子”，第二年为“乙丑”，第三年为“丙寅”… …依此类推，排列到“癸酉”后，天干回到“甲”重新开始，即“甲戌”“乙亥”，之后地支回到“子”重新开始，即“丙子”… …依此类推.1911年中国爆发推翻清朝专制帝制、建立共和政体的全国性革命,这一年是辛亥年，史称“辛亥革命”.1949新中国成立，请推算新中国成立的年份为( )

A.己丑年B.己酉年

C.丙寅年D.甲寅年

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，将等腰直角三角形沿斜边上的高翻折，使二面角的大小为，翻折后的中点为.