Question

【题目】已知圆的方程:

（1）求m的取值范围；

（2）若圆C与直线相交于,两点，且,求的值

（3）若(1)中的圆与直线x＋2y－4＝0相交于M、N两点，且OM⊥ON(O为坐标原点)，求m的值；

Answer 1

【答案】(1);(2);(3).

【解析】

试题分析：(1)圆的方程要满足;或配成圆的标准方程，;

(2) 利用弦心距公式，先求点到面的距离，利用 ，求出的值;

(3)设,若,那么,利用直线方程与圆的方程联立，得到根与系数的关系式，代入后，求得的值.

试题解析：解：（1）(1)方程x2＋y2－2x－4y＋m＝0，可化为

(x－1)2＋(y－2)2＝5－m，

∵此方程表示圆，

∴5－m＞0，即m＜5.

(2) 圆的方程化为 ，圆心 C（1，2），半径 ，

则圆心C（1，2）到直线的距离为

由于，则，有，

得.

（3）

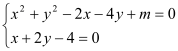
消去x得(4－2y)2＋y2－2×(4－2y)－4y＋m＝0，

化简得5y2－16y＋m＋8＝0.

设M(x1，y1)，N(x2，y2)，则

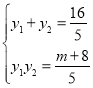
①②

由OM⊥ON得y1y2＋x1x2＝0

即y1y2＋(4－2y1)(4－2y2)＝0，

∴16－8(y1＋y2)＋5y1y2＝0.

将①②两式代入上式得

16－8×＋5×＝0，

解之得.