
【题目】记![]() (
(![]() ,
,![]() ).
).
(1)求函数![]() 的零点;
的零点;
(2)设![]() 、
、![]() 、
、![]() 均为正整数,且
均为正整数,且![]() 为最简根式,若存在
为最简根式,若存在![]() ,使得
,使得![]() 可唯一表示为
可唯一表示为![]() 的形式(
的形式(![]() ),求证:
),求证:![]() ;
;
(3)已知![]() ,是否存在
,是否存在![]() ,使得
,使得![]()
成立,若存在,试求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() ;(2)证明略;(3)存在.
;(2)证明略;(3)存在.
【解析】
(1)写出F(x)的解析式,解方程F(x)=0,可得零点;
(2)由题意可得![]() ,
,![]() ,两式相乘可得证明。
,两式相乘可得证明。
(3)由条件可得t+s=ts,假设存在n1∈N*,使得![]() 成立,化简整理求出满足条件的t,s和n1的值。
成立,化简整理求出满足条件的t,s和n1的值。
(1)函数F(x)=f2(x-1)-1=(x-1)2-1,x>1,
由F(x)=0,解得x=2(0舍去),
即有F(x)的零点为2
(2)证明:若存在n0∈N*,
使得![]() 可唯一表示为
可唯一表示为![]() 的形式(
的形式(![]() )
)
即有![]() ,
,![]()
两式相乘可得|ξ2-η2μ|n0=T-(T-1)=1
可得|ξ2-η2μ|=1
(3)假设存在n1∈N*,使得![]() 成立
成立
由f-1(t)+f-1(s)=1,可得t-1+s-1=1,即t+s=ts
由假设可得![]()
即为![]()
即有![]()
可取t=s=2,n1可取一切正整数,上式成立。
则存在n1∈N*,使得![]() 成立
成立


科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=4,∠A=60°,以对角线BD为折痕把△ABD折起,使点A到达如图所示点E的位置,使![]() .
.
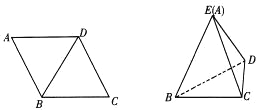
(1)求证:BD⊥EC;
(2)求三棱锥B-CE-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 满足:对任何
满足:对任何![]() ,都有
,都有![]() ,且当
,且当![]() 时,
时,![]() ,在下列结论中,正确命题的序号是________
,在下列结论中,正确命题的序号是________
① 对任何![]() ,都有
,都有![]() ;② 函数
;② 函数![]() 的值域是
的值域是![]() ;
;
③ 存在![]() ,使得
,使得![]() ;④ “函数
;④ “函数![]() 在区间
在区间![]() 上单调递减”的充要条
上单调递减”的充要条
件是“存在![]() ,使得
,使得![]() ”;
”;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(![]() )天的销售价格(单位:元/件)为
)天的销售价格(单位:元/件)为![]() ,第x天的销售量(单位:件)为
,第x天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
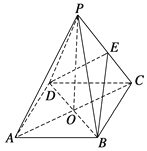
【题目】如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:平面PAC⊥平面BDE;
(2)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足x3<y3,则下列不等式中恒成立的是( )
A. (![]() )x>(
)x>(![]() )y B. ln(x2+1)>ln(y2+1)
)y B. ln(x2+1)>ln(y2+1)
C. ![]() D. tanx>tany
D. tanx>tany
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com