
【题目】已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,椭圆上任意一点
,椭圆上任意一点![]() ,满足
,满足![]() ,且椭圆过点
,且椭圆过点![]() .
.
(1)求椭圆的标准方程;
(2)设![]() 是轨迹
是轨迹![]() 上的两个动点,线段
上的两个动点,线段![]() 的中点
的中点![]() 在直线
在直线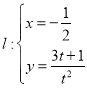 (为参数)上,线段
(为参数)上,线段![]() 的中垂线与
的中垂线与![]() 交于
交于![]() 两点,是否存在点
两点,是否存在点![]() ,使以
,使以![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出
,若存在,求出![]() 点坐标,若不存在,请说明理由.
点坐标,若不存在,请说明理由.
【答案】(1) ![]() (2) 存在点
(2) 存在点![]() 符合条件,坐标为
符合条件,坐标为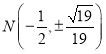 .
.
【解析】
(1)设![]() ,
,![]() ,
,![]() ,根据题意列出方程,联立求解即可;
,根据题意列出方程,联立求解即可;
(2)直线![]() 参数方程转换为普通方程,当直线
参数方程转换为普通方程,当直线![]() 垂直于
垂直于![]() 轴时,三点共线不符合题意;当直线
轴时,三点共线不符合题意;当直线![]() 不垂直与
不垂直与![]() 轴时,设存在点
轴时,设存在点![]()
![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,根据题意利用圆的性质和垂直向量点积为0,列出方程求解可得答案.
,根据题意利用圆的性质和垂直向量点积为0,列出方程求解可得答案.
解:(1)设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,
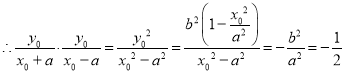
![]() 椭圆过点
椭圆过点![]() ,
,![]() ②
②
联立①②解得: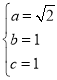
所求椭圆方程为:![]()
(2)将直线的参数方程![]() :
: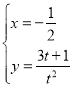 (
(![]() 为参数)化为普通方程
为参数)化为普通方程![]() ,
,
当直线![]() 垂直于
垂直于![]() 轴时,直线
轴时,直线![]() 方程为
方程为![]() :
:![]() ,
,
此时![]() ,
,![]() 与点
与点![]() 三点共线,不合题意;
三点共线,不合题意;
当直线![]() 不垂直与
不垂直与![]() 轴时,设存在点
轴时,设存在点![]()
![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
由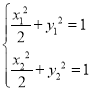 得:
得:![]() ,则
,则![]() ,故
,故![]()
此时,直线![]() 斜率为
斜率为![]() ,
,![]() 的直线方程为
的直线方程为![]() ,即
,即![]()
联立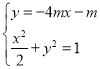 ,整理得:
,整理得:![]()
所以![]() ,
,![]()
由题意![]() ,于是
,于是
![]()
![]()
![]()
![]()
![]() ,因为
,因为![]() 在椭圆内,
在椭圆内,![]() ,
,![]() 符合题意;
符合题意;
综上,存在点![]() 符合条件,坐标为
符合条件,坐标为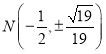 .
.


科目:高中数学 来源: 题型:
【题目】在甲地,随着人们生活水平的不断提高,进入电影院看电影逐渐成为老百姓的一种娱乐方式.我们把习惯进入电影院看电影的人简称为“有习惯”的人,否则称为“无习惯的人”.某电影院在甲地随机调查了100位年龄在15岁到75岁的市民,他们的年龄的频数分布和“有习惯”的人数如下表:

(1)以年龄45岁为分界点,请根据100个样本数据完成下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“有习惯”的人与年龄有关;
的把握认为“有习惯”的人与年龄有关;

(2)已知甲地从15岁到75岁的市民大约有11万人,以频率估计概率,若每张电影票定价为![]() 元
元![]() ,则在“有习惯”的人中约有
,则在“有习惯”的人中约有![]() 的人会买票看电影(
的人会买票看电影(![]() 为常数).已知票价定为30元的某电影,票房达到了 69.3万元.某新影片要上映,电影院若将电影票定价为25元,那么该影片票房估计能达到多少万元?
为常数).已知票价定为30元的某电影,票房达到了 69.3万元.某新影片要上映,电影院若将电影票定价为25元,那么该影片票房估计能达到多少万元?
参考公式:![]() ,其中
,其中![]() .
.
参考临界值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂抽取了一台设备![]() 在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.

(1)计算该样本的平均值![]() ,方差
,方差![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(2)根据长期生产经验,可以认为这台设备在正常状态下生产的产品的质量指标值服从正态分布![]() ,其中
,其中![]() 近似为样本平均值,
近似为样本平均值,![]() 近似为样本方差
近似为样本方差![]() .任取一个产品,记其质量指标值为
.任取一个产品,记其质量指标值为![]() .若
.若![]() ,则认为该产品为一等品;
,则认为该产品为一等品;![]() ,则认为该产品为二等品;若
,则认为该产品为二等品;若![]() ,则认为该产品为不合格品.已知设备
,则认为该产品为不合格品.已知设备![]() 正常状态下每天生产这种产品1000个.
正常状态下每天生产这种产品1000个.
(i)用样本估计总体,问该工厂一天生产的产品中不合格品是否超过![]() ?
?
(ii)某公司向该工厂推出以旧换新活动,补足50万元即可用设备![]() 换得生产相同产品的改进设备
换得生产相同产品的改进设备![]() .经测试,设备
.经测试,设备![]() 正常状态下每天生产产品1200个,生产的产品为一等品的概率是
正常状态下每天生产产品1200个,生产的产品为一等品的概率是![]() ,二等品的概率是
,二等品的概率是![]() ,不合格品的概率是
,不合格品的概率是![]() .若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备
.若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备![]() ?
?
参考数据:①![]() ;②
;②![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
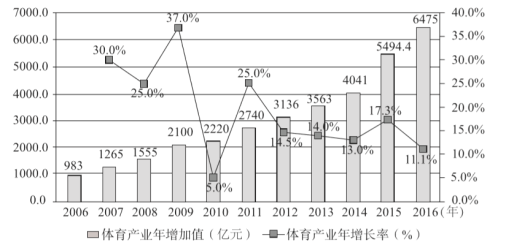
(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多![]() 亿元以上的概率;
亿元以上的概率;
(Ⅱ)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(Ⅲ)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象局统计,某市2019年从1月1日至1月30日这30天里有26天出现雾霾天气.国际上通常用环境空气质量指数(AQI)来描述污染状况,下表是某气象观测点记录的连续4天里,该市AQI指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() 的情况.
的情况.
AQI指数 | 900 | 700 | 300 | 100 |
空气水平可见度 | 0.5 | 3.5 | 6.5 | 9.5 |
(1)设![]() ,根据表中的数据,求出
,根据表中的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若某天该市AQT指数![]() ,那么当天空气水平可见度大约为多少?
,那么当天空气水平可见度大约为多少?
附:参考数据:![]() ,
,![]() .
.
参考公式:线性回归力程![]() 中,
中,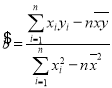 ,
,![]() ,其中
,其中![]() 为样本平均数.
为样本平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com