
【题目】已知![]() p:
p:![]() ,q:
,q:![]() .
.
(1)若p是q充分不必要条件,求实数![]() 的取值范围;
的取值范围;
(2)若“非p”是“非q”的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ax2+bx,(a,b∈R).
(1)设a=1,f(x)在x=1处的切线过点(2,6),求b的值;
(2)设b=a2+2,求函数f(x)在区间[1,4]上的最大值;
(3)定义:一般的,设函数g(x)的定义域为D,若存在x0∈D,使g(x0)=x0成立,则称x0为函数g(x)的不动点.设a>0,试问当函数f(x)有两个不同的不动点时,这两个不动点能否同时也是函数f(x)的极值点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为1m的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形ABCD为中心在圆心的矩形,现计划将矩形ABCD区域设计为可推拉的窗口. 
(1)若窗口ABCD为正方形,且面积大于 ![]() m2(木条宽度忽略不计),求四根木条总长的取值范围;
m2(木条宽度忽略不计),求四根木条总长的取值范围;
(2)若四根木条总长为6m,求窗口ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9这9个数字中取3个偶数和4个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)在(1)中的七位数中,偶数排在一起,奇数也排在一起的有多少个?
(3)在(1)中任意2个偶数都不相邻的七位数有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为1m的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形ABCD为中心在圆心的矩形,现计划将矩形ABCD区域设计为可推拉的窗口. 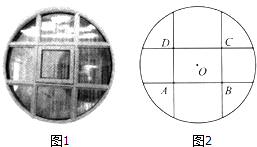
(1)若窗口ABCD为正方形,且面积大于 ![]() m2(木条宽度忽略不计),求四根木条总长的取值范围;
m2(木条宽度忽略不计),求四根木条总长的取值范围;
(2)若四根木条总长为6m,求窗口ABCD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为万元. 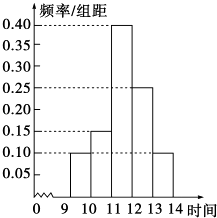
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50名学生组成一个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ……,第五组
……,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)请估计学校1800名学生中,成绩属于第四组的人数;
(2)若成绩小于15秒认为良好,求该样本中在这次百米测试中成绩良好的人数;
(3)请根据频率分布直方图,求样本数据的众数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ,现建立以
,现建立以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系.
轴的正半轴为极轴的极坐标系.
(1)写出直线![]() 极坐标方程,曲线
极坐标方程,曲线![]() 的参数方程;
的参数方程;
(2)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间(t),结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间t(分钟/人) | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分钟开始准备第三位顾客的泡茶工具的概率;
(2)用X表示至第4分钟末已准备好了工具的顾客人数,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com