
ЁОЬтФПЁПЃЈ14ЗжЃЉвбжЊaЃЌbЮЊГЃЪ§ЃЌЧвaЁй0ЃЌКЏЪ§fЃЈxЃЉ=Љax+b+axlnxЃЌfЃЈeЃЉ=2ЃЈe=2.71828ЁЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЎ
ЃЈIЃЉЧѓЪЕЪ§bЕФжЕЃЛ
ЃЈIIЃЉЧѓКЏЪ§fЃЈxЃЉЕФЕЅЕїЧјМфЃЛ
ЃЈIIIЃЉЕБa=1ЪБЃЌЪЧЗёЭЌЪБДцдкЪЕЪ§mКЭMЃЈmЃМMЃЉЃЌЪЙЕУЖдУПвЛИіtЁЪ[mЃЌM]ЃЌжБЯпy=tгыЧњЯпy=fЃЈxЃЉЃЈxЁЪ[![]() ЃЌe]ЃЉЖМгаЙЋЙВЕуЃПШєДцдкЃЌЧѓГізюаЁЕФЪЕЪ§mКЭзюДѓЕФЪЕЪ§MЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЌe]ЃЉЖМгаЙЋЙВЕуЃПШєДцдкЃЌЧѓГізюаЁЕФЪЕЪ§mКЭзюДѓЕФЪЕЪ§MЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈIЃЉb=2
ЃЈIIЃЉЕБaЃО0ЪБЃЌКЏЪ§fЃЈxЃЉЕФЕЅЕїЕндіЧјМфЮЊЃЈ1ЃЌ+ЁоЃЉЃЌЕЅЕїЕнМѕЧјМфЮЊЃЈ0ЃЌ1ЃЉЃЛ
ЕБaЃМ0ЪБЃЌКЏЪ§fЃЈxЃЉЕФЕЅЕїЕндіЧјМфЮЊЃЈ0ЃЌ1ЃЉЃЌЕЅЕїЕнМѕЧјМфЮЊЃЈ1ЃЌ+ЁоЃЉЃЛ
ЃЈIIIЃЉМћНтЮі
ЁОНтЮіЁП
ЪдЬтЃЈIЃЉАбx=eДњШыКЏЪ§fЃЈxЃЉ=Љax+b+axlnxЃЌНтЗНГЬМДПЩЧѓЕУЪЕЪ§bЕФжЕЃЛ
ЃЈIIЃЉЧѓЕМЃЌВЂХаЖЯЕМЪ§ЕФЗћКХЃЌШЗЖЈКЏЪ§ЕФЕЅЕїЧјМфЃЛ
ЃЈIIIЃЉМйЩшДцдкЪЕЪ§mКЭMЃЈmЃМMЃЉЃЌЪЙЕУЖдУПвЛИіtЁЪ[mЃЌM]ЃЌжБЯпy=tгыЧњЯпy=fЃЈxЃЉЃЈxЁЪ[![]() ЃЌe]ЃЉЖМгаЙЋЙВЕуЃЌзЊЛЏЮЊРћгУЕМЪ§ЧѓКЏЪ§y=fЃЈxЃЉдкЧјМф[
ЃЌe]ЃЉЖМгаЙЋЙВЕуЃЌзЊЛЏЮЊРћгУЕМЪ§ЧѓКЏЪ§y=fЃЈxЃЉдкЧјМф[![]() ЃЌe]ЩЯЕФжЕгђЃЎ
ЃЌe]ЩЯЕФжЕгђЃЎ
НтЃКЃЈIЃЉгЩfЃЈeЃЉ=2ЃЌДњШыfЃЈxЃЉ=Љax+b+axlnxЃЌ
ЕУb=2ЃЛ
ЃЈIIЃЉгЩЃЈIЃЉПЩЕУfЃЈxЃЉ=Љax+2+axlnxЃЌКЏЪ§fЃЈxЃЉЕФЖЈвхгђЮЊЃЈ0ЃЌ+ЁоЃЉЃЌ
ДгЖјfЁфЃЈxЃЉ=alnxЃЌ
ЁпaЁй0ЃЌЙЪ
ЂйЕБaЃО0ЪБЃЌгЩfЁфЃЈxЃЉЃО0ЕУxЃО1ЃЌгЩfЁфЃЈxЃЉЃМ0ЕУ0ЃМxЃМ1ЃЛ
ЂкЕБaЃМ0ЪБЃЌгЩfЁфЃЈxЃЉЃО0ЕУ0ЃМxЃМ1ЃЌгЩfЁфЃЈxЃЉЃМ0ЕУxЃО1ЃЛ
злЩЯЃЌЕБaЃО0ЪБЃЌКЏЪ§fЃЈxЃЉЕФЕЅЕїЕндіЧјМфЮЊЃЈ1ЃЌ+ЁоЃЉЃЌЕЅЕїЕнМѕЧјМфЮЊЃЈ0ЃЌ1ЃЉЃЛ
ЕБaЃМ0ЪБЃЌКЏЪ§fЃЈxЃЉЕФЕЅЕїЕндіЧјМфЮЊЃЈ0ЃЌ1ЃЉЃЌЕЅЕїЕнМѕЧјМфЮЊЃЈ1ЃЌ+ЁоЃЉЃЛ
ЃЈIIIЃЉЕБa=1ЪБЃЌfЃЈxЃЉ=Љx+2+xlnxЃЌfЁфЃЈxЃЉ=lnxЃЌ
гЩЃЈIIЃЉПЩЕУЃЌЕБxЁЪЃЈ![]() ЃЌeЃЉЃЌfЃЈxЃЉЃЌfЁфЃЈxЃЉБфЛЏЧщПіШчЯТБэЃК
ЃЌeЃЉЃЌfЃЈxЃЉЃЌfЁфЃЈxЃЉБфЛЏЧщПіШчЯТБэЃК
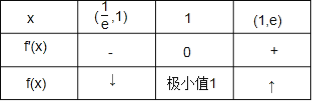
гжfЃЈ![]() ЃЉ=2Љ
ЃЉ=2Љ![]() ЃМ2ЃЌ
ЃМ2ЃЌ
Ыљвдy=fЃЈxЃЉдк[![]() ЃЌe]ЩЯЕФжЕгђЮЊ[1ЃЌ2]ЃЌ
ЃЌe]ЩЯЕФжЕгђЮЊ[1ЃЌ2]ЃЌ
ОнДЫПЩЕУЃЌШє![]() ЃЌдђЖдУПвЛИіtЁЪ[mЃЌM]ЃЌжБЯпy=tгыЧњЯпy=fЃЈxЃЉЃЈxЁЪ[
ЃЌдђЖдУПвЛИіtЁЪ[mЃЌM]ЃЌжБЯпy=tгыЧњЯпy=fЃЈxЃЉЃЈxЁЪ[![]() ЃЌe]ЃЉЖМгаЙЋЙВЕуЃЛ
ЃЌe]ЃЉЖМгаЙЋЙВЕуЃЛ
ВЂЧвЖдУПвЛИіtЁЪЃЈЉЁоЃЌmЃЉЁШЃЈMЃЌ+ЁоЃЉЃЌжБЯпy=tгыЧњЯпy=fЃЈxЃЉЃЈxЁЪ[![]() ЃЌe]ЃЉЖМУЛгаЙЋЙВЕуЃЛ
ЃЌe]ЃЉЖМУЛгаЙЋЙВЕуЃЛ
злЩЯЕБa=1ЪБЃЌДцдкзюаЁЪЕЪ§m=1КЭзюДѓЕФЪЕЪ§M=2ЃЈmЃМMЃЉЃЌЪЙЕУЖдУПвЛИіtЁЪ[mЃЌM]ЃЌжБЯпy=tгыЧњЯпy=fЃЈxЃЉЃЈxЁЪ[![]() ЃЌe]ЃЉЖМгаЙЋЙВЕуЃЎ
ЃЌe]ЃЉЖМгаЙЋЙВЕуЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЭждВЃК![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌyжсгкЭждВЯрНЛгкAЁЂBСНЕуЃЌ
ЃЌyжсгкЭждВЯрНЛгкAЁЂBСНЕуЃЌ![]() ЃЌCЁЂDЪЧЭждВЩЯвьгкAЁЂBЕФШЮвтСНЕуЃЌЧвжБЯпACЁЂBDЯрНЛгкЕуMЃЌжБЯпADЁЂBCЯрНЛгкЕуNЃЎ
ЃЌCЁЂDЪЧЭждВЩЯвьгкAЁЂBЕФШЮвтСНЕуЃЌЧвжБЯпACЁЂBDЯрНЛгкЕуMЃЌжБЯпADЁЂBCЯрНЛгкЕуNЃЎ
![]() ЧѓЭждВЕФЗНГЬЃЛ
ЧѓЭждВЕФЗНГЬЃЛ
![]() ЧѓжБЯпMNЕФаБТЪЃЎ
ЧѓжБЯпMNЕФаБТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌИУМИКЮЬхЪЧгЩвЛИіжБШ§РтжљADEЉBCFКЭвЛИіе§ЫФРтзЖPЉABCDзщКЯЖјГЩЃЌADЁЭAFЃЌAE=AD=2ЃЎ
ЃЈЂёЃЉжЄУїЃКЦНУцPADЁЭЦНУцABFEЃЛ
ЃЈЂђЃЉЧѓе§ЫФРтзЖPЉABCDЕФИпhЃЌЪЙЕУЖўУцНЧCЉAFЉPЕФгрЯвжЕЪЧ ![]() ЃЎ
ЃЎ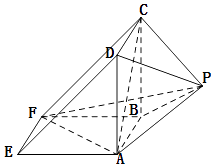
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФНЙЕугыЫЋЧњЯп
ЕФНЙЕугыЫЋЧњЯп![]() ЕФНЙЕужиКЯЃЌВЂЧвОЙ§Еу
ЕФНЙЕужиКЯЃЌВЂЧвОЙ§Еу![]() .
.
ЃЈЂёЃЉЧѓЭждВCЕФБъзМЗНГЬЃЛ
ЃЈIIЃЉ ЩшЭждВCЖЬжсЕФЩЯЖЅЕуЮЊPЃЌжБЯп![]() ВЛОЙ§PЕуЧвгы
ВЛОЙ§PЕуЧвгы![]() ЯрНЛгк
ЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌШєжБЯпPAгыжБЯпPBЕФаБТЪЕФКЭЮЊ
СНЕуЃЌШєжБЯпPAгыжБЯпPBЕФаБТЪЕФКЭЮЊ![]() ЃЌХаЖЯжБЯп
ЃЌХаЖЯжБЯп![]() ЪЧЗёЙ§ЖЈЕуЃЌШєЪЧЃЌЧѓГіетИіЖЈЕуЃЌЗёдђЫЕУїРэгЩ.
ЪЧЗёЙ§ЖЈЕуЃЌШєЪЧЃЌЧѓГіетИіЖЈЕуЃЌЗёдђЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпEЃКy2=8xЃЌдВMЃКЃЈxЉ2ЃЉ2+y2=4ЃЌЕуNЮЊХзЮяЯпEЩЯЕФЖЏЕуЃЌOЮЊзјБъдЕуЃЌЯпЖЮONЕФжаЕуPЕФЙьМЃЮЊЧњЯпCЃЎ
ЃЈ1ЃЉЧѓЧњЯпCЕФЗНГЬЃЛ
ЃЈ2ЃЉЕуQЃЈx0 ЃЌ y0ЃЉЃЈx0Ён5ЃЉЪЧЧњЯпCЩЯЕФЕуЃЌЙ§ЕуQзїдВMЕФСНЬѕЧаЯпЃЌЗжБ№гыxжсНЛгкAЃЌBСНЕуЃЌЧѓЁїQABУцЛ§ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЖЈвхдкRЩЯЕФПЩЕМКЏЪ§fЃЈxЃЉЕФЕМКЏЪ§ЮЊfЁфЃЈxЃЉЃЌШєfЃЈ3ЃЉ=1ЃЌЧв3fЃЈxЃЉ+xfЁфЃЈxЃЉЃОlnЃЈx+1ЃЉЃЌдђВЛЕШЪНЃЈxЉ2017ЃЉ3fЃЈxЉ2017ЃЉЉ27ЃО0ЕФНтМЏЮЊЃЈ ЃЉ
A.ЃЈ2014ЃЌ+ЁоЃЉ
B.ЃЈ0ЃЌ2014ЃЉ
C.ЃЈ0ЃЌ2020ЃЉ
D.ЃЈ2020ЃЌ+ЁоЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХЭјТчгЊЯњКЭЕчзгЩЬЮёЕФаЫЦ№ЃЌШЫУЧЕФЙКЮяЗНЪНИќОпЖрбљЛЏЃЌФГЕїВщЛњЙЙЫцЛњГщШЁ10УћЙКЮяепНјааВЩЗУЃЌ5УћФаадЙКЮяепжага3УћЧуЯђгкбЁдёЭјЙКЃЌ2УћЧуЯђгкбЁдёЪЕЬхЕъЃЌ5УћХЎадЙКЮяепжага2УћЧуЯђгкбЁдёЭјЙКЃЌ3УћЧуЯђгкбЁдёЪЕЬхЕъЃЎ
ЃЈ1ЃЉШєДг10УћЙКЮяепжаЫцЛњГщШЁ2УћЃЌЦфжаФаЁЂХЎИївЛУћЃЌЧѓжСЩй1УћЧуЯђгкбЁдёЪЕЬхЕъЕФИХТЪЃЛ
ЃЈ2ЃЉШєДгет10УћЙКЮяепжаЫцЛњГщШЁ3УћЃЌЩшXБэЪОГщЕНЧуЯђгкбЁдёЭјЙКЕФФаадЙКЮяепЕФШЫЪ§ЃЌЧѓXЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§Са{an}ЕФИїЯюОљЮЊе§Ъ§ЃЌЦфЧАnЯюКЭЮЊSn ЃЌ вбжЊ ![]()
![]() =1ЃЌЧвa1=
=1ЃЌЧвa1= ![]() ЃЌдђtanSnЕФШЁжЕМЏКЯЪЧЃЈ ЃЉ
ЃЌдђtanSnЕФШЁжЕМЏКЯЪЧЃЈ ЃЉ
A.{0ЃЌ ![]() }
}
B.{0ЃЌ ![]() ЃЌ
ЃЌ ![]() }
}
C.{0ЃЌ ![]() ЃЌЉ
ЃЌЉ ![]() }
}
D.{0ЃЌ ![]() ЃЌЉ
ЃЌЉ ![]() }
}
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЧјМф[x1 ЃЌ x2]ЕФГЄЖШЮЊx2Љx1ЃЈx2ЃОx1ЃЉЕЅЕїЕндіЃЉЃЌКЏЪ§ ![]() ЃЈaЁЪRЃЌaЁй0ЃЉЕФЖЈвхгђгыжЕгђЖМЪЧ[mЃЌn]ЃЈnЃОmЃЉЃЌдђЧјМф[mЃЌn]ШЁзюДѓГЄЖШЪБЪЕЪ§aЕФжЕЃЈ ЃЉ
ЃЈaЁЪRЃЌaЁй0ЃЉЕФЖЈвхгђгыжЕгђЖМЪЧ[mЃЌn]ЃЈnЃОmЃЉЃЌдђЧјМф[mЃЌn]ШЁзюДѓГЄЖШЪБЪЕЪ§aЕФжЕЃЈ ЃЉ
A.![]()
B.Љ3
C.1
D.3
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com