
【题目】今年冬天流感盛行,据医务室统计,北校近30天每天因病请假人数依次构成数列 ![]() ,已知
,已知 ![]() ,
, ![]() ,且
,且 ![]() ,则这30天因病请假的人数共有人.
,则这30天因病请假的人数共有人.
【答案】![]()
【解析】∵a1=1,a2=2,且an+2-an=1+(-1)n (n∈N*),
∴a3-a1=1+(-1)1=0,
∴a3=a1=1,
∴a4-a2=1+(-1)2=2,解得a4=a2+2=4;
同理可得,a29=a27=…=a3=a1=1;
a6=6,a8=8,…,a30=30,
显然,a2、a4、…、a30构成以2为首项,2为公差的等差数列,共15项,
∴这30天因病请假的人数共有:
S30=(a1+a3+…+a29)+(a2+a4+…+a30)=15+ ![]()
故答案为:255
根据数列的递推式先求出前几项的值,观察规律:n为奇数时,an为1;n为偶数时,an是以2为首项,2为公差的等差数列,最后根据等差数列的前n项和共和即可求出结果。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|(x﹣2)(x+3)<0},B={x|y= ![]() },则A∩(RB)=( )
},则A∩(RB)=( )
A.[﹣3,﹣1]
B.(﹣3,﹣1]
C.(﹣3,﹣1)
D.[﹣1,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列 ![]() 有无穷项,且每一项均为自然数,若75,99,235为
有无穷项,且每一项均为自然数,若75,99,235为 ![]() 中的项,则下列自然数中一定是
中的项,则下列自然数中一定是 ![]() 中的项的是( )
中的项的是( )
A.2017
B.2019
C.2021
D.2023
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为
的右焦点为 ![]() ,且点
,且点 ![]() 在椭圆
在椭圆 ![]() 上.
上.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过椭圆 ![]() 上异于其顶点的任意一点
上异于其顶点的任意一点 ![]() 作圆
作圆 ![]() 的两条切线,切点分别为
的两条切线,切点分别为 ![]() (
( ![]() 不在坐标轴上),若直线
不在坐标轴上),若直线 ![]() 在
在 ![]() 轴,
轴, ![]() 轴上的截距分别为
轴上的截距分别为 ![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
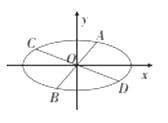
【题目】椭圆 ![]() 的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为
的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为 ![]() .
.
(1)若一条直径的斜率为 ![]() ,求该直径的共轭直径所在的直线方程;
,求该直径的共轭直径所在的直线方程;
(2)若椭圆的两条共轭直径为 ![]() 和
和 ![]() ,它们的斜率分别为
,它们的斜率分别为 ![]() ,证明:四边形
,证明:四边形 ![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半径为![]() 的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池![]() 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰![]() ,其中
,其中![]() 为圆心,
为圆心, ![]() 在圆的直径上,
在圆的直径上, ![]() 在半圆周上,如图.
在半圆周上,如图.
(1)设![]() ,征地面积为
,征地面积为![]() ,求
,求![]() 的表达式,并写出定义域;
的表达式,并写出定义域;
(2)当![]() 满足
满足![]() 取得最大值时,开发效果最佳,求出开发效果最佳的角
取得最大值时,开发效果最佳,求出开发效果最佳的角![]() 的值,
的值,
求出![]() 的最大值.
的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com