
【题目】(江苏省南通市2018届高三最后一卷 --- 备用题数学试题)已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对任意的实数
对任意的实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .
.
(2) ![]() .
.
(3) ![]() .
.
【解析】
(1)首先将![]() 代入函数解析式,求出函数的导数,求出函数的切线的斜率,利用点斜式写出直线的方程,化简求得结果;
代入函数解析式,求出函数的导数,求出函数的切线的斜率,利用点斜式写出直线的方程,化简求得结果;
(2)求出函数的导数,利用函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() 是方程
是方程![]() 的两个不等正根,韦达定理得到关系,将
的两个不等正根,韦达定理得到关系,将![]() 化为关于
化为关于![]() 的函数关系式,利用导数求得结果;
的函数关系式,利用导数求得结果;
(3)将恒成立问题应用导数来研究,分类讨论,求得结果.
(1)当![]() 时,
时,![]() ,故
,故![]() ,
,
且![]() ,故
,故![]()
所以函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(2)由![]() ,
,![]() 可得
可得![]()
因为函数![]() 存在两个极值点
存在两个极值点![]() ,所以
,所以![]() 是方程
是方程![]() 的两个不等正根,
的两个不等正根,
即![]() 的两个不等正根为
的两个不等正根为![]()
所以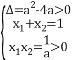 ,即
,即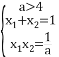
![]()
所以![]()
![]()
令![]() ,故
,故![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
故![]() 得取值范围是
得取值范围是![]()
(3)据题意,![]() 对任意的实数
对任意的实数![]() 恒成立,
恒成立,
即![]() 对任意的实数
对任意的实数![]() 恒成立.
恒成立.
令![]() ,则
,则![]()
①若![]() ,当
,当![]() 时,
时,![]() ,故
,故![]() 符合题意;
符合题意;
②若![]() ,
,
(i)若![]() ,即
,即![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调赠
上单调赠
所以当![]() 时,
时,![]() ,故
,故![]() 符合题意;
符合题意;
(ii)若![]() ,即
,即![]() ,令
,令![]() ,得
,得![]() (舍去),
(舍去),
![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调减;
上单调减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以存在![]() ,使得
,使得![]() ,与题意矛盾,
,与题意矛盾,
所以![]() 不符题意.
不符题意.
③若![]() ,令
,令![]() ,得
,得![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调增;当
上单调增;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调减.
上单调减.
首先证明:![]()
要证:![]() ,即要证:
,即要证:![]() ,只要证:
,只要证:![]()
因为![]() ,所以
,所以![]() ,故
,故![]()
所以![]()
其次证明,当![]() 时,
时,![]() 对任意的
对任意的![]() 都成立
都成立
令![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,则
,则![]()
所以当![]() 时,
时,![]() 对任意的
对任意的![]() 都成立
都成立
所以当![]() 时,
时,![]()
即![]() ,与题意矛盾,故
,与题意矛盾,故![]() 不符题意,
不符题意,
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).
(1)求抛物线C的方程及准线l的方程;
(2)过焦点F的直线(不经过Q点)与抛物线交于A,B两点,与准线l交于点M,记QA,QB,QM的斜率分别为k1 , k2 , k3 , 问是否存在常数λ,使得k1+k2=λk3成立?若存在λ,求出λ的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】眉山市位于四川西南,有“千载诗书城,人文第一州”的美誉,这里是大文豪苏轼、苏洵、苏辙的故乡,也是人们旅游的好地方.在今年的国庆黄金周,为了丰富游客的文化生活,每天在东坡故里三苏祠举行“三苏文化”知识竞赛.已知甲、乙两队参赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
,![]() ,
,![]() ,且各人回答正确与否相互之间没有影响.
,且各人回答正确与否相互之间没有影响.
(1)分别求甲队总得分为0分;2分的概率;
(2)求甲队得2分乙队得1分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电商的快速发展,快递业突飞猛进,到目前,中国拥有世界上最大的快递市场.某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,在收费10元的基础上,每超过
的包裹,在收费10元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
该公司将最近承揽的100件包裹的重量统计如下:

公司对近60天,每天揽件数量统计如下表:

以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来5天内恰有2天揽件数在101~300之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②根据以往的经验,公司将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前前台有工作人员3人,每人每天揽件不超过150件,日工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1= ![]() ,an+1﹣1=an(an﹣1)(n∈N*)且Sn=
,an+1﹣1=an(an﹣1)(n∈N*)且Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,则Sn的整数部分的所有可能值构成的集合是( )
,则Sn的整数部分的所有可能值构成的集合是( )
A.{0,1,2}
B.{0,1,2,3}
C.{1,2}
D.{0,2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知f(x+1)=x2+4x+1,求f(x)的解析式.
(2)已知f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9.求f(x).
(3)已知f(x)满足2f(x)+f ![]() =3x,求f(x).
=3x,求f(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() 是某公共汽车线路收支差额
是某公共汽车线路收支差额![]() 元与乘客量
元与乘客量![]() 的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的方案,根据图
的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的方案,根据图![]() 上点
上点![]() 、点
、点![]() 以及射线
以及射线![]() 上的点的实际意义,用文字说明图
上的点的实际意义,用文字说明图![]() 方案是______,图
方案是______,图![]() 方案是______.
方案是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com